Nuprl Basics - NonCanonical Forms - continued from Computation

IF YOU CAN SEE THIS go to /sfa/Nuprl/Shared/Xindentation_hack_doc.html

NonCanonical Forms - continued from Computation

Here we list the NonCanonical forms and indicate how they evaluate, except for forms that operate specifically on numeric literals or token literals; for those, see Integers and Atoms.

Destructors are operators that break down complex expressions having canonical form, and continue computing on those parts. Here are our primitive destructors:

InjCase(inl(a); u. c(u); v. d(v)) * c(a)
InjCase(inr(b); u. c(u); v. d(v)) * d(b)
Case of nil; nil  b ; x.xs, rec:v  f(x;xs;v) * b
Case of a.as; nil  b ; x.xs, rec:v  f(x;xs;v)
*
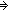
f(a;as;Case of as; nil  b ; x.xs, rec:v  f(x;xs;v))
<a,b>/c,d. f(c;d) * f(a;b)
(x.b(x))(a) * b(a)

Each of these rewrites has the following significance. For any closed instance of the rewrite, to evaluate the left-hand side, one evaluates the right hand side.

These forms on the left-hand sides are called "redexes" and are said to "reduce" to their "contractums" shown on the right-hand side. In these destructor forms, the place filled by the term to be analyzed is called a "principal argument" place, which means that it is evaluated in place before the resulting redex is evaluated.

It is also possible to have operators that compute regardless of the form of the arguments.

recind(a; f,x. g(f;x)) * g(x.recind(x; f,x. g(f;x));a)

There is also a rather degenerate and unnecessary noncanonical form that ignores its argument and has no value at all, namely "any(x)". It is a vestige of another, older type system.

See Canonical Forms.

(March 2001 - sfa )

About:

IF YOU CAN SEE THIS go to /sfa/Nuprl/Shared/Xindentation_hack_doc.html

NuprlPrimitives Sections NuprlLIB Doc