Concise Informal Annotations - titles, paraphrases, domains, roles

If the only utility for search were based on formal content, one utility which is indeed essential to using a formal library or archives, then searching for formal content from an informal starting point would be constrained to judging (often guessing) what formal expressions were likely used for informal concepts. As valuable as this utility would be, it could not be considered adequate.

The inclusion of "Readings" in the FDL will provide explanatory Texts that consist largely of words that have embedded in them references to formal objects they are about. So by employing a content search on words and phrases we could find these explanatory texts, and by reading them ascertain the relevant formal objects. This too is a valuable capacity, but there are three notable inefficiencies in this method: reading a relatively large text that may discuss and relate several formal objects in order to discern which are relevant to the search is not automated; if one simply assumes that all the formal objects may be relevant in order to apply automation instead of reading, this is inefficient in a different way because one must often expect the assumption to be wrong; and lastly, the production of explanatory material of the sort we imagine as part of readings is itself rather expensive, and is not likely always to "reach" all the formal content reliably.

These problems would be mitigated by concise informal annotations of formal objects. Each "concise" annotation would be about one object, and would consist of informal words or phrases. This addresses each of the three inefficiencies mentioned above. Concise annotation focuses the search and "reaches" more formal material since it's cheaper and less distracting to create than discourse.

Two typical kinds of concise annotations are titles and paraphrases. Often theorems, concepts, or programs have conventional titles which should therefore be attached to their formalizations. For example "Ramsey's Theorem", "Dedekind Infinite", and "Dijkstra's Shortest Path Algorithm". The paraphrases used as concise annotations would not normally be "read off" the formal expression, but rather would complement the formal detail. For example, one might paraphrase

Thm* k:, q1,q2:, r1,r2:k. q1k+r1 = q2k+r2  q1 = q2 & r1 = r2

as "Integer division is unique", or paraphrase

Thm* as,bs,cs:T List. ((as @ bs) @ cs) = (as @ (bs @ cs))

as "List catenation is associative" or "Appending lists is associative". Some theorems may be unworthy of paraphrase such as

Thm* n:, as:A List(n). ||as|| = n  

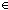
whose obvious paraphrase, "Lists of a given length have that length", is silly. If you want to find a lemma like this, it would be because you were looking for theorems relating the formal expressions " List()" and "||||" and you would already be in the formal domain.

Amanda Holland-Minkley advises me that these annotations, and others, useful to search are also useful for proof paraphrasing. The reason is that while one may develop methods for paraphrasing proof structures principally by analyzing the structure of the proof and recognizing forms that can be reorganized into conventional verbal forms, one gets down to a level where the proper paraphrase is simply not derivable from the internal structure. When a proof is paraphrased one may want to cite a lemma by conventional title or to paraphrase its content in a way that is not easily determined by its formal structure. Further annotations that are concise and useful for search and paraphrasing are indications of intended domain, and the role in the larger body of material, such as whether a theorem is intended simply as a lemma for citation by a particular proof rather than of broader interest, or whether it is simply a technical device for facilitating formal proof rather than having a more general cognitive significance. IF YOU CAN SEE THIS go to http://www.cs.cornell.edu/Info/People/sfa/Nuprl/Shared/Xindentation_hack_doc.html