Nuprl Lemma : double_neg_elim
( P:
P: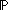 . (
. (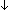 P
P 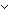 (
(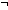 P)))
P))) 
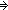 (
( P:
P: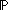 . ((
. ((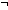
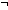
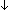 P)
P) 
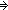 (
(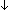 P)))
P)))
Proof
Definitions occuring in Statement :
prop: 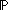 ,
all:
,
all:  x:A. B[x],
not:
x:A. B[x],
not: 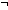 A,
squash:
A,
squash: 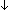 T,
implies: P
T,
implies: P 
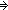 Q,
or: P
Q,
or: P 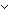 Q
Q
Definitions :
implies: P 
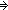 Q,
all:
Q,
all:  x:A. B[x],
prop:
x:A. B[x],
prop: 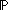 ,
squash:
,
squash: 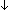 T,
member: t
T,
member: t 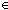 T,
true: True,
so_lambda:
T,
true: True,
so_lambda: 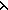
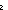 x.t[x],
not:
x.t[x],
not: 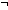 A,
false: False,
or: P
A,
false: False,
or: P 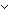 Q,
uall:
Q,
uall:  [x:A]. B[x],
so_apply: x[s]
[x:A]. B[x],
so_apply: x[s]
Lemmas :
not_wf,
squash_wf,
all_wf,
or_wf
(\mforall{}P:\mBbbP{}. (\mdownarrow{}P \mvee{} (\mneg{}P))) {}\mRightarrow{} (\mforall{}P:\mBbbP{}. ((\mneg{}\mneg{}\mdownarrow{}P) {}\mRightarrow{} (\mdownarrow{}P)))
Date html generated:
2013_03_20-AM-10_48_51
Last ObjectModification:
2013_02_25-PM-04_58_24
Home
Index