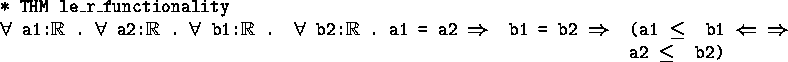Since 
is a proper subset of Seq(
) it is necessary to
prove that the operations above actually produce real numbers. In Nuprl such
``well-formedness'' proofs are generally required and usually trivial. With the
constructive reals, though, these proofs are anything but
routine, and in fact are the reason that the definitions are so complicated.
Thus the following theorems deserve to be mentioned:
Another concern is that functions are well defined with respect to real equality. That is, they do not depend on the particular sequences representing their arguments. For example, the canonical bound of a number is not functional.
This theorem is not quite as trivial as it looks --- the equality on the left is rational equality whereas the one on the right is real equality.
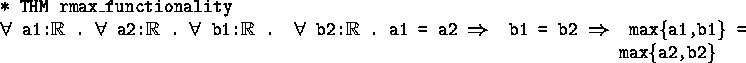
Similarly the order relations are well defined:
