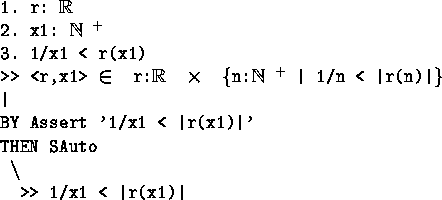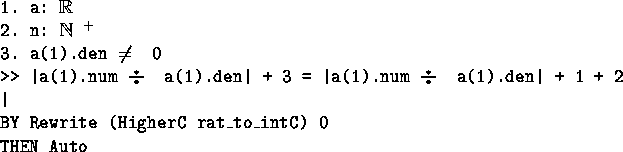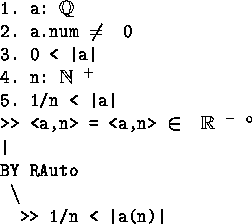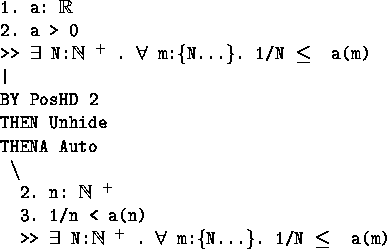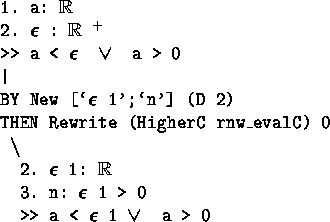Next: Tactic Code
Up: Formalizing Constructive Real Analysis
Previous: The Intermediate Value
The following is a listing of the user defined tactics in the rational and real
libraries together with illustrations of their use. Some do a fair amount of
computation or rewriting while others are basically macros for various
sequences of tactics that show up repeatedly in the libraries. ``Direct
computation'' tactics perform only term reduction and unfolding and folding of
definitions.
- CaseSplit
- This tactic decomposes an ifthenelse term and
rewrites the Boolean condition to a proposition. From qabsval_le_q:
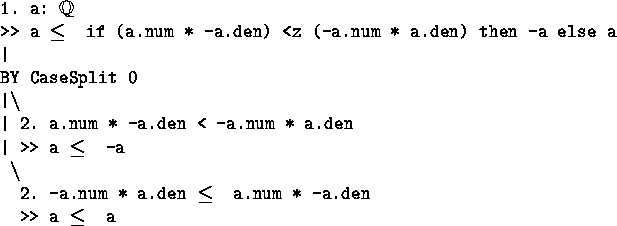
- qnd_evalC
- This is a direct computation tactic that reduces
a/b.num to a and a/b.den to b. From eq_q_refl:

- expon_unrollC
- This unrolls the definition of expon using
direct computation.

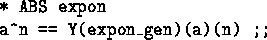
The effect is to replace a^n with if n =z 1 then a else (a *Ã
a^(n - 1)). From expon_preserves_pos:

- lt_q_expand
- Converts a < b to a.num * b.den < b.num *
a.den. le_q_expand and eq_q_expand are similar. From
lt_q_qmax:

- qabsval_evalC
- This tactic rewrites absolute values of rational
arithmetic expressions to expressions with absolute values in the numerators.
From rat_triangle:

- SAuto
- This is a version of the autotactic that tries calling
AbSetMemEqTypeCD. It is useful for handling membership goals of the form
a = b
 T where T is a set type. From real_pos_inc:
T where T is a set type. From real_pos_inc:
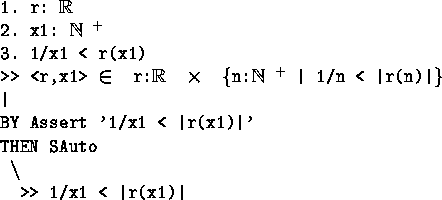
- rat_to_intC
- Rewrites expressions of rational integers (rationals
of the form a/1) to integer expressions. In the example, from
canon_bound_property, the conclusion is an equality between rationals.
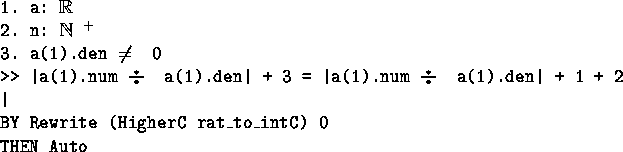
- int_to_ratC
- Rewrites integer expressions to rational ones.
- RAuto
- Like SAuto except that if it gets stuck on a membership
goal it will try to unfold the type subterm. It is useful for goals like
a = b
 where the type needs unfolding. From
rat_nzero_to_real_nzero:
where the type needs unfolding. From
rat_nzero_to_real_nzero:
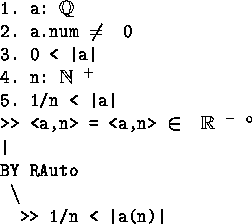
- PosHD
- Decomposes a hypothesis of the form a > 0 and obtains a
witness, although it sometimes must be used with the tactic Unhide. From
real_pos_lemma:
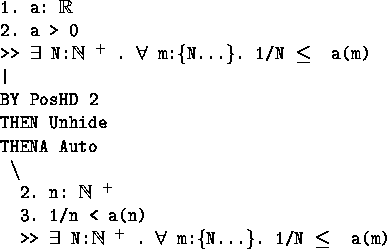
- PosCD
- This takes a term as an argument to be used as a witness for a
goal of the form a > 0. From rneg_functionality_wrt_lt_r:

- rnw_evalC
- This tactic is similar to qnd_evalC except that it
takes pairs which are nonzero reals. In this example from
pos_quasi_decidable the term
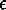 in the conclusion is actually a
display for rnum(
in the conclusion is actually a
display for rnum(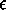 ), which becomes rnum(<
), which becomes rnum(<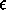 1,n>)
after (D 2) is applied.
1,n>)
after (D 2) is applied.
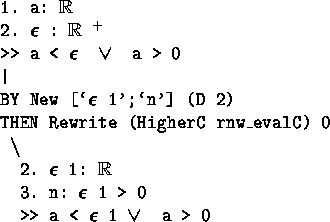
- real_apply_evalC
- This direct computation tactic takes a real
expression applied to a natural number, and ``distributes'' the application
inside the expression according to the definitions of the operations involved.
The operations it knows about are radd, rneg, rsub,
real_rat, rmul_gen, rmax and rabsval. From
radd_preserves_pos:

- real_to_ratC
- Rewrites expressions of reals which are constant
sequences to rational expressions.
- rat_to_realC
- Rewrites rational expressions to real expressions,
but does not recognize qinv or qdiv. The reason for this is that
rinv and rdiv must be given nonzero reals, requiring witnesses.
In this example from halving_to_zero the conclusion is a rational
expression. It gets converted to a real expression and then is decomposed so
that it matches hypothesis 7.

- rat_to_real_witnessC
- Same as rat_to_realC except that it
handles qinv and qdiv. It takes a natural number to be used as a
witness for all instances of rinv and rdiv. This tactic does not
get used in the library so we have a cooked up example:




Next: Tactic Code
Up: Formalizing Constructive Real Analysis
Previous: The Intermediate Value
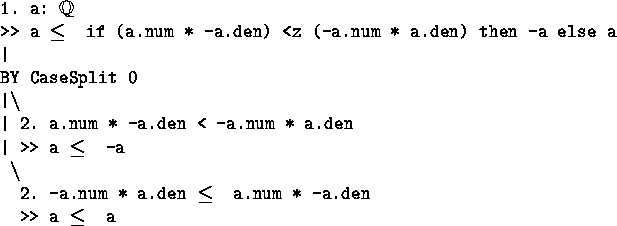

![]()
![]()



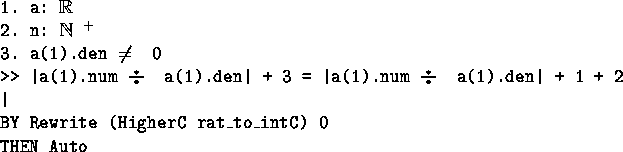
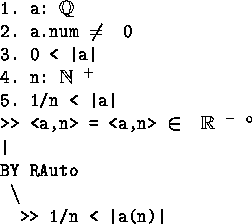
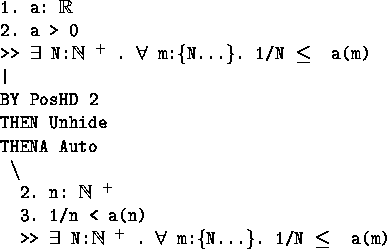

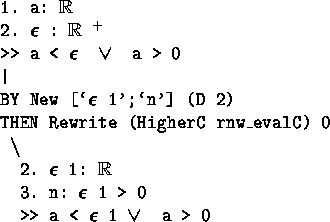



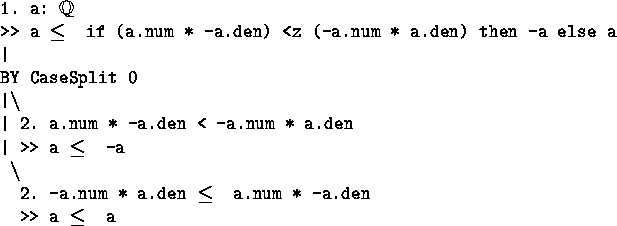

![]()
![]()