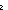
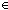
The Type of Booleans

Thm* true  

Thm* false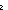  

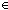
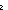
Thm* b:. b = true  b = false

There is a conditional expression whose execution branches on values:

if X t else r fi

if true t else r fi * t

if false t else r fi * r

It happens that is not primitive, but there is rarely need for users to know this. See Deriving Bool.

A lot of Tactic support has been developed for . It is intimately related to constructive decidability.

The Nuprl logic is "constructive" and does not assume that every proposition is either true or false, even when well-defined (see Propositions).
More acutely, there is no method computationally for branching on the truth or falsity of an arbitrary proposition. So, where one would be inclined to branch on the truth value of a proposition, one instead attempts to formulate the concepts using the type instead of the type Prop; this is not always possible.

To mediate between the type of booleans and the type of propositions, we employ a coercion operator,

Def b == if b True else False fi

where True and False are standard true and false propositions.

Normally, except when showing definitions, we suppress the display of the coercion operator itself because it is usually clear whether a boolean or a propositional expression is needed, and it becomes noisy to read. The well-formedness theorem for this coercion is Thm* b:. b  Prop. The aptness of making the Prop coercion operator invisible is accentuated when we consider that we are in theory free to add true and false as new propositions themselves, which would put them directly into Prop and make a subtype of Prop, thus eliminating the need for defining a coercion operator at all.

Here is a sample theorem employing the (invisible) coercion operator to relate Propositional conjunction to boolean conjunction (Def pq == if p q else false fi):

Thm* p,q:. (pq)  p & q.

Here are the implicit -to-Prop coercions in this theorem statement:

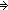
p,q:. (pq)  p & q.

About: IF YOU CAN SEE THIS go to /sfa/Nuprl/Shared/Xindentation_hack_doc.html