IF YOU CAN SEE THIS go to /sfa/Nuprl/Shared/Xindentation_hack_doc.html
Thm*  a:
a: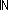 , b:
, b: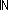
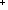 .
. 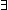 q:
q: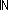 , r:
, r: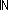 b. a = q
b. a = q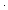 b+r
b+r
To show this, we hold b 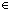
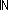
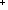 constant while we do induction over a
constant while we do induction over a 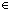
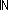 to prove
to prove
 a:
a: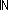 .
. 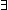 q:
q: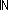 , r:
, r: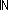 b. a = q
b. a = q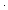 b+r.
b+r.
We use the true-for-less form of induction, assuming
 a1:
a1: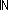 . a1<a
. a1<a 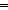
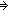 (
(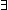 q:
q: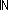 , r:
, r: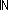 b. a1 = q
b. a1 = q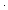 b+r)
b+r)
and attempt to show 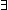 q:
q: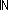 , r:
, r: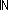 b. a = q
b. a = q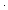 b+r.
b+r.
If a<b then just use a for r, and 0 for q.
Otherwise, a-b 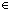
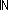 and a-b<a, so by our induction hyp,
and a-b<a, so by our induction hyp,
a-b = q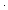 b+r for some q
b+r for some q 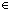
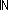 , r
, r 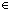
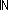 b,
b,
so, a-b = q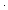 b+r, from which follows a = (q+1)
b+r, from which follows a = (q+1)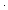 b+r,
b+r,
which show our goal to be satisfied using q+1 for q.
QED
About:
IF YOU CAN SEE THIS go to /sfa/Nuprl/Shared/Xindentation_hack_doc.html
![]()
![]()
![]()
![]()
![]()
a:
.
q:
, r:
b. a = q
b+r
a1:
. a1<a
(
q:
, r:
b. a1 = q
b+r)
![]() q:
q:![]() , r:
, r:![]() b. a = q
b. a = q![]() b+r
b+r![]()
![]()
b+r
b
![]() b+r
b+r![]() b+r
b+r