Selected Objects
| def | auto_iso | A1  A2
== A2
==  f:(S1 f:(S1 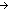 S2).
Bij(S1; S2; f)
& ( S2).
Bij(S1; S2; f)
& ( s:S1, a:Alph. f( s:S1, a:Alph. f(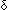 A1(s,a)) = A1(s,a)) = 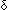 A2(f(s),a))
& f(InitialState(A1)) = InitialState(A2)
& ( A2(f(s),a))
& f(InitialState(A1)) = InitialState(A2)
& ( s:S1. FinalState(A1)(s) = FinalState(A2)(f(s)) s:S1. FinalState(A1)(s) = FinalState(A2)(f(s)) 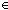 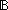 ) ) |
| THM | auto_iso_sym |  A1:Automata(Alph;S1), A2:Automata(Alph;S2). A1 A1:Automata(Alph;S1), A2:Automata(Alph;S2). A1  A2 A2 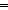  A2 A2  A1 A1 |
| def | refine | A1 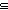 A2 == A2 ==  x,y:Alph*. (Result(A1)x) = (Result(A1)y) x,y:Alph*. (Result(A1)x) = (Result(A1)y) 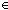 S1 S1 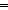  (Result(A2)x) = (Result(A2)y) (Result(A2)x) = (Result(A2)y) 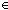 S2 S2 |
| def | connected | Con(A) ==  s:St. s:St.  l:Alph*. (Result(A)l) = s l:Alph*. (Result(A)l) = s |
| def | card_le | |S| 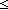 |T| == |T| ==  f:(S f:(S 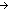 T). Inj(S; T; f) T). Inj(S; T; f) |
| def | card_ge | |S|  |T| == |T| ==  f:(S f:(S 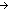 T). Surj(S; T; f) T). Surj(S; T; f) |
| COM | le_vs_ge_com | '|S| 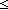 |T|' does not imply '|T| |T|' does not imply '|T|  |S|' |S|' |
| THM | refine_ge |  A1:Automata(Alph;S1), A2:Automata(Alph;S2). Con(A1) & Con(A2) A1:Automata(Alph;S1), A2:Automata(Alph;S2). Con(A1) & Con(A2) 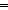  A1 A1 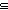 A2 A2 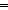  |S1| |S1|  |S2| |S2| |
| THM | refine_iso |  A1:Automata(Alph;S1), A2:Automata(Alph;S2).
Con(A1) & Con(A2) A1:Automata(Alph;S1), A2:Automata(Alph;S2).
Con(A1) & Con(A2) 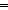  LangOf(A1) = LangOf(A2) LangOf(A1) = LangOf(A2) 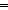  A1 A1 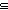 A2 & A2 A2 & A2 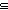 A1 A1 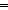  A1 A1  A2 A2 |
| def | lang_auto | A(g) == < (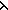 s,a. a.s),nil,g > s,a. a.s),nil,g > |
| THM | lang_auto_compute |  L:LangOver(Alph), g:((x,y:Alph*//(x L-induced Equiv y)) L:LangOver(Alph), g:((x,y:Alph*//(x L-induced Equiv y)) 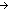 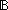 ), l:Alph*.
(Result(A(g))l) = l ), l:Alph*.
(Result(A(g))l) = l 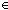 x,y:Alph*//(x L-induced Equiv y) x,y:Alph*//(x L-induced Equiv y) |
| THM | lang_auto_lem |  L:LangOver(Alph), g:((x,y:Alph*//(x L-induced Equiv y)) L:LangOver(Alph), g:((x,y:Alph*//(x L-induced Equiv y)) 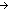 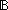 ).
( ).
( l:Alph*. L(l) l:Alph*. L(l)   g(l)) g(l)) 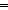  LangOf(A(g)) = L LangOf(A(g)) = L |
| THM | lang_auto_is_min |  Auto:Automata(Alph;St), g:((x,y:Alph*//(x LangOf(Auto)-induced Equiv y)) Auto:Automata(Alph;St), g:((x,y:Alph*//(x LangOf(Auto)-induced Equiv y)) 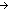 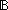 ). Auto ). Auto 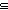 A(g) A(g) |
| THM | homo_init |  Auto:Automata(Alph;St), g:((x,y:Alph*//(x LangOf(Auto)-induced Equiv y)) Auto:Automata(Alph;St), g:((x,y:Alph*//(x LangOf(Auto)-induced Equiv y)) 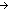 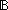 ), c:(St ), c:(St 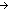 Alph*).
( Alph*).
( q:St. (Result(Auto)c(q)) = q) q:St. (Result(Auto)c(q)) = q) 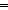  c(InitialState(Auto)) = nil
c(InitialState(Auto)) = nil 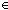 x,y:Alph*//(x LangOf(Auto)-induced Equiv y) x,y:Alph*//(x LangOf(Auto)-induced Equiv y) |
| THM | homo_step |  Auto:Automata(Alph;St), g:((x,y:Alph*//(x LangOf(Auto)-induced Equiv y)) Auto:Automata(Alph;St), g:((x,y:Alph*//(x LangOf(Auto)-induced Equiv y)) 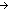 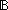 ), c:(St ), c:(St 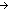 Alph*).
( Alph*).
( q:St. (Result(Auto)c(q)) = q) q:St. (Result(Auto)c(q)) = q) 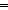  (
( q:St, a:Alph. c( q:St, a:Alph. c(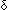 Auto(q,a)) = Auto(q,a)) = 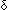 A(g)(c(q),a) A(g)(c(q),a) 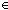 x,y:Alph*//(x LangOf(Auto)-induced Equiv y)) x,y:Alph*//(x LangOf(Auto)-induced Equiv y)) |