Selected Objects
| def | auto1 | Auto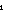 == < ( == < ( s,a. s),0,( s,a. s),0,( s.true s.true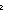 ) > ) > |
| THM | auto1_minimization |  n: n: , f:( , f:( n n 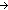 (x,y: (x,y: 2*//(x LangOf(Auto 2*//(x LangOf(Auto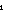 )-induced Equiv y))).
Bij( )-induced Equiv y))).
Bij( n; x,y: n; x,y: 2*//(x LangOf(Auto 2*//(x LangOf(Auto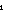 )-induced Equiv y); f) )-induced Equiv y); f) |
| COM | auto1_howto | If you want to get number of state in minimal automata
that accepts the same language as 'Auto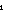 ' just type
term_to_string (evaluate_term 'ext{auto1_minimization}')
into your ML top loop. But keep in mind that in order
to get 'ext{auto1_minimization}' you will need to open
a term slot with Ctrl+o and type in "auto1_minimization".
In several minutes you will get lots of line as output.
Just look for a first number! ' just type
term_to_string (evaluate_term 'ext{auto1_minimization}')
into your ML top loop. But keep in mind that in order
to get 'ext{auto1_minimization}' you will need to open
a term slot with Ctrl+o and type in "auto1_minimization".
In several minutes you will get lots of line as output.
Just look for a first number! |
| def | auto2 | Auto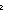 == < ( == < ( s,a. 2-s),0,( s,a. 2-s),0,( s.s= s.s=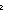 0) > 0) > |
| THM | auto2_minimization |  n: n: , f:( , f:( n n 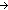 (x,y: (x,y: 2*//(x LangOf(Auto 2*//(x LangOf(Auto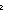 )-induced Equiv y))).
Bij( )-induced Equiv y))).
Bij( n; x,y: n; x,y: 2*//(x LangOf(Auto 2*//(x LangOf(Auto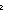 )-induced Equiv y); f) )-induced Equiv y); f) |
| def | auto3 | Auto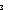 == < ( == < ( s,a. a),0,( s,a. a),0,( s.s= s.s=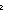 0) > 0) > |
| THM | auto3_minimization |  n: n: , f:( , f:( n n 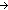 (x,y: (x,y: 3*//(x LangOf(Auto 3*//(x LangOf(Auto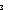 )-induced Equiv y))).
Bij( )-induced Equiv y))).
Bij( n; x,y: n; x,y: 3*//(x LangOf(Auto 3*//(x LangOf(Auto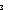 )-induced Equiv y); f) )-induced Equiv y); f) |
| def | auto3_1 | Auto3_1 == < ( s,a. a),0,( s,a. a),0,( s.true s.true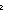 ) > ) > |
| THM | auto3_1_minimization |  n: n: , f:( , f:( n n 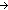 (x,y: (x,y: 1*//(x LangOf(Auto3_1)-induced Equiv y))).
Bij( 1*//(x LangOf(Auto3_1)-induced Equiv y))).
Bij( n; x,y: n; x,y: 1*//(x LangOf(Auto3_1)-induced Equiv y); f) 1*//(x LangOf(Auto3_1)-induced Equiv y); f) |
| def | auto3_2 | Auto3_2 == < ( s,a. a),0,( s,a. a),0,( s.true s.true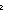 ) > ) > |
| THM | auto3_2_minimization |  n: n: , f:( , f:( n n 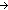 (x,y: (x,y: 2*//(x LangOf(Auto3_2)-induced Equiv y))).
Bij( 2*//(x LangOf(Auto3_2)-induced Equiv y))).
Bij( n; x,y: n; x,y: 2*//(x LangOf(Auto3_2)-induced Equiv y); f) 2*//(x LangOf(Auto3_2)-induced Equiv y); f) |
| def | auto3_23 | auto3_23() == < ( s,a. a),0,( s,a. a),0,( s.true s.true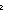 ) > ) > |
| THM | auto3_23_minimization |  n: n: , f:( , f:( n n 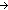 (x,y: (x,y: 2*//(x LangOf(auto3_23())-induced Equiv y))).
Bij( 2*//(x LangOf(auto3_23())-induced Equiv y))).
Bij( n; x,y: n; x,y: 2*//(x LangOf(auto3_23())-induced Equiv y); f) 2*//(x LangOf(auto3_23())-induced Equiv y); f) |
| def | auto3_3 | auto3_3() == < ( s,a. a),0,( s,a. a),0,( s.true s.true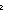 ) > ) > |
| THM | auto3_3_minimization |  n: n: , f:( , f:( n n 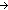 (x,y: (x,y: 3*//(x LangOf(auto3_3())-induced Equiv y))).
Bij( 3*//(x LangOf(auto3_3())-induced Equiv y))).
Bij( n; x,y: n; x,y: 3*//(x LangOf(auto3_3())-induced Equiv y); f) 3*//(x LangOf(auto3_3())-induced Equiv y); f) |
| def | auto4 | Auto4 == < ( s,a. 1-s),0,( s,a. 1-s),0,( s.s= s.s=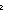 0) > 0) > |
| THM | auto4_minimization |  n: n: , f:( , f:( n n 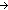 (x,y: (x,y: 2*//(x LangOf(Auto4)-induced Equiv y))).
Bij( 2*//(x LangOf(Auto4)-induced Equiv y))).
Bij( n; x,y: n; x,y: 2*//(x LangOf(Auto4)-induced Equiv y); f) 2*//(x LangOf(Auto4)-induced Equiv y); f) |
| def | auto_oddeven | OddEven#n == < ( s: s: (2 (2 n). n).  a: a: n. (s+(2 n. (s+(2 a)) rem (2 a)) rem (2 n)),0,( n)),0,( s: s: (2 (2 n). s= n). s=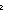 0 0 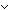 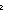 s= s=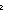 (2 (2 n)-1) > n)-1) > |
| THM | oddeven_minimization |  n: n:  . .
 k: k: , f:( , f:( k k 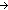 (x,y: (x,y: n*//(x LangOf(OddEven#n)-induced Equiv y))).
Bij( n*//(x LangOf(OddEven#n)-induced Equiv y))).
Bij( k; x,y: k; x,y: n*//(x LangOf(OddEven#n)-induced Equiv y); f) n*//(x LangOf(OddEven#n)-induced Equiv y); f) |