Selected Objects
| def | min_ar | (rec) MinAr(f;i;n) == if (f(n-i))=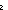 (f(n)) (f(n))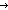 i else MinAr(f;i-1;n) fi i else MinAr(f;i-1;n) fi |
| THM | min_ar_alt |  f:( f:(    ), n: ), n: , i: , i: (n+1), j: (n+1), j: (n-i+1). f(n-i) = f(n) (n-i+1). f(n-i) = f(n) 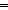 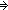 MinAr(f;j+i;n) = MinAr(f;j;n-i)+i MinAr(f;j+i;n) = MinAr(f;j;n-i)+i |
| THM | min_ar_sound |  f:( f:(    ), n: ), n: , i: , i: (n+1). f(n-MinAr(f;i;n)) = f(n) (n+1). f(n-MinAr(f;i;n)) = f(n) |
| def | min_arg | MinArg(f : {0..n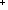 }) == n-MinAr(f;n;n) }) == n-MinAr(f;n;n) |
| THM | min_arg_unique |  f:( f:(    ), n,k: ), n,k: . f(n) = f(k) . f(n) = f(k) 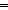 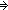 MinArg(f : {0..n MinArg(f : {0..n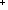 }) = MinArg(f : {0..k }) = MinArg(f : {0..k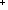 }) }) 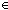  |
| THM | min_arg_sound |  f:( f:(    ), n: ), n: . f(MinArg(f : {0..n . f(MinArg(f : {0..n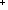 })) = f(n) })) = f(n) |
| THM | min_arg_iff |  f:( f:(    ), n,k: ), n,k: . f(n) = f(k) . f(n) = f(k) 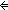 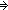 MinArg(f : {0..n MinArg(f : {0..n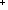 }) = MinArg(f : {0..k }) = MinArg(f : {0..k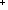 }) }) 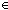  |
| def | min_el | Min{ x | xEn } == MinArg(E(n) : {0..n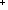 }) }) |
| THM | equiv_rel_fun |  E:(T E:(T  T T   ), s,t:T. (EquivRel x,y:T. x E y) ), s,t:T. (EquivRel x,y:T. x E y) 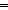 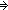 (s E t) (s E t) 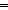 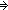 E(s) = E(t) E(s) = E(t) |
| THM | min_el_unique |  E:( E:(       ), n,k: ), n,k: . (EquivRel x,y: . (EquivRel x,y: . x E y) . x E y) 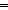 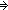 (n E k) (n E k) 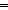 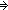 Min{ x | xEn } = Min{ x | xEk } Min{ x | xEn } = Min{ x | xEk } |
| THM | min_el_sound |  E:( E:(       ), n: ), n: . (EquivRel x,y: . (EquivRel x,y: . x E y) . x E y) 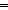 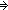 (n E Min{ x | xEn }) (n E Min{ x | xEn }) |
| THM | min_el_iff |  E:( E:(       ), n,k: ), n,k: . (EquivRel x,y: . (EquivRel x,y: . x E y) . x E y) 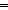 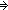 ((n E k) ((n E k) 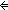 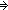 Min{ x | xEn } = Min{ x | xEk }) Min{ x | xEn } = Min{ x | xEk }) |
| THM | decide_imp_bool |  R:(T R:(T  T T  Prop). ( Prop). ( x,y:T. Dec(x R y)) x,y:T. Dec(x R y)) 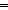 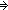 ( (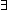 r:(T r:(T  T T   ). ).  x,y:T. (x r y) x,y:T. (x r y) 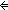 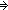 (x R y)) (x R y)) |
| THM | comp_choice |  E:( E:(      Prop).
(EquivRel x,y: Prop).
(EquivRel x,y: . x E y) & ( . x E y) & ( x,y: x,y: . Dec(x E y)) . Dec(x E y)) 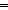 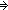 (
(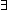 h:( h:(    ). ( ). ( n,k: n,k: . (n E k) . (n E k) 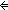 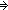 h(n) = h(k)) & ( h(n) = h(k)) & ( n: n: . n E (h(n)))) . n E (h(n)))) |