Selected Objects
| def | automata | Automata(Alph;States) == (States 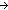 Alph Alph 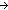 States) States) States States (States (States 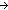 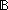 ) ) |
| def | DA_act | 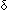 a == 1of(a) a == 1of(a) |
| def | DA_init | InitialState(a) == 1of(2of(a)) |
| def | DA_fin | FinalState(a) == 2of(2of(a)) |
| def | compute_list | (rec) Result(DA)l == if null(l)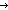 InitialState(DA) else InitialState(DA) else 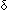 DA((Result(DA)tl(l)),hd(l)) fi DA((Result(DA)tl(l)),hd(l)) fi |
| THM | compute_list_qwf |  Auto:Automata(Alph;St), l:x,y:Alph*//((Result(Auto)x) = (Result(Auto)y)). (Result(Auto)l) Auto:Automata(Alph;St), l:x,y:Alph*//((Result(Auto)x) = (Result(Auto)y)). (Result(Auto)l) 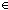 St St |
| THM | compute_l_inv |  Auto:Automata(Alph;St), x,y,z:Alph*.
(Result(Auto)x) = (Result(Auto)y) Auto:Automata(Alph;St), x,y,z:Alph*.
(Result(Auto)x) = (Result(Auto)y)   (Result(Auto)z @ x) = (Result(Auto)z @ y) (Result(Auto)z @ x) = (Result(Auto)z @ y) |
| def | accept_list | DA(l)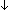 == FinalState(DA)(Result(DA)l) == FinalState(DA)(Result(DA)l) |
| THM | accept_list_qwf |  Auto:Automata(Alph;St), l:x,y:Alph*//((Result(Auto)x) = (Result(Auto)y)). Auto(l) Auto:Automata(Alph;St), l:x,y:Alph*//((Result(Auto)x) = (Result(Auto)y)). Auto(l)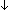 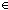 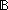 |
| def | auto_lang | LangOf(DA)(l) == DA(l)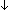 |
| THM | action_auto |  Auto:Automata(Alph;St), l:Alph*. ( < St, Auto:Automata(Alph;St), l:Alph*. ( < St, l,s. l,s. 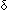 Auto(s,l) > :l Auto(s,l) > :l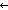 InitialState(Auto)) = (Result(Auto)l) InitialState(Auto)) = (Result(Auto)l) |
| THM | pos_states |  Auto:Automata(Alph;St). Fin(St) Auto:Automata(Alph;St). Fin(St)   ( ( n: n: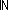 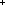 . #(St)=n ) . #(St)=n ) |
| THM | reach_lemma |  S:ActionSet(Alph), si:S.car, nn: S:ActionSet(Alph), si:S.car, nn: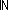 , f:( , f:(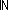 nn nn 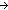 Alph), g:(Alph Alph), g:(Alph 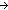 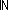 nn).
Fin(S.car) nn).
Fin(S.car)   InvFuns(
InvFuns(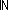 nn; Alph; f; g) nn; Alph; f; g)   (
( n: n: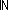 . .
 RL:{y:{x:(S.car*)| 0 < ||x|| & ||x|| RL:{y:{x:(S.car*)| 0 < ||x|| & ||x||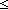 n+1 }| y[(||y||-1)] = si }.
( n+1 }| y[(||y||-1)] = si }.
( s:S.car. ( s:S.car. ( w:Alph*. (S:w w:Alph*. (S:w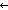 si) = s) si) = s) 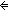  mem_f(S.car;s;RL)) mem_f(S.car;s;RL))
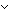 ||RL|| = n+1
& ( ||RL|| = n+1
& ( i: i: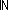 ||RL||, j: ||RL||, j: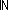 i. i.  RL[i] = RL[j])
& ( RL[i] = RL[j])
& ( s:S.car. mem_f(S.car;s;RL) s:S.car. mem_f(S.car;s;RL)   ( ( w:Alph*. (S:w w:Alph*. (S:w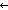 si) = s))
& ( si) = s))
& ( k: k: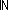 .
k .
k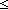 nn nn   (
( RLa:S.car*.
( RLa:S.car*.
( i:{1..||RL|| i:{1..||RL|| }, a:Alph. mem_f(S.car;S.act(a,RL[i]);RL) }, a:Alph. mem_f(S.car;S.act(a,RL[i]);RL) 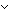 mem_f(S.car;S.act(a,RL[i]);RLa))
& ( mem_f(S.car;S.act(a,RL[i]);RLa))
& ( a:Alph. g(a) < k a:Alph. g(a) < k   mem_f(S.car;S.act(a,hd(RL));RL) mem_f(S.car;S.act(a,hd(RL));RL) 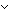 mem_f(S.car;S.act(a,hd(RL));RLa))
& ( mem_f(S.car;S.act(a,hd(RL));RLa))
& ( s:S.car. mem_f(S.car;s;RLa) s:S.car. mem_f(S.car;s;RLa)   ( ( w:Alph*. (S:w w:Alph*. (S:w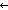 si) = s))))) si) = s))))) |
| THM | reach_aux |  S:ActionSet(Alph), si:S.car.
Fin(S.car) S:ActionSet(Alph), si:S.car.
Fin(S.car)   Fin(Alph) Fin(Alph)   ( ( RL:S.car*. RL:S.car*.  s:S.car. ( s:S.car. ( w:Alph*. (S:w w:Alph*. (S:w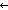 si) = s) si) = s) 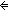  mem_f(S.car;s;RL)) mem_f(S.car;s;RL)) |
| THM | reach_list |  Auto:Automata(Alph;St).
Fin(St) & Fin(Alph) Auto:Automata(Alph;St).
Fin(St) & Fin(Alph)   ( ( RL:St*. RL:St*.  s:St. ( s:St. ( w:Alph*. (Result(Auto)w) = s) w:Alph*. (Result(Auto)w) = s) 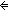  mem_f(St;s;RL)) mem_f(St;s;RL)) |
| THM | reach_dec |  Auto:Automata(Alph;St). Fin(Alph) Auto:Automata(Alph;St). Fin(Alph)   Fin(St) Fin(St)   ( ( s:St. Dec( s:St. Dec( w:Alph*. (Result(Auto)w) = s)) w:Alph*. (Result(Auto)w) = s)) |