Thm*  x,y: x,y: , n: , n:  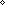 . ((x+y) rem n) = (((x rem n)+(y rem n)) rem n)+if (x+y < . ((x+y) rem n) = (((x rem n)+(y rem n)) rem n)+if (x+y < 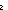 0) 0)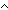 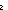 (0 < (0 < 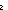 (((x rem n)+(y rem n)) rem n)) (((x rem n)+(y rem n)) rem n)) -|n| ;((((x rem n)+(y rem n)) rem n) < -|n| ;((((x rem n)+(y rem n)) rem n) < 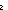 0) 0)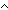 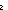 (0 < (0 < 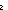 x+y) x+y) |n| else 0 fi |n| else 0 fi | [rem_add] |
Thm*  x: x: , n: , n: 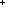 . ((-x) mod n) = if (x mod n)= . ((-x) mod n) = if (x mod n)=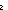 0 0 0 else n-(x mod n) fi 0 else n-(x mod n) fi | [mod_minus] |
Thm*  i: i: . f91(i) ~ if 101 < . f91(i) ~ if 101 < 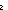 i i i-10 else 91 fi i-10 else 91 fi | [f91-val] |
Thm*  k: k: , f,g:( , f,g:( k k   ), p:( ), p:( k k   ). sum(if p(i) ). sum(if p(i) f(i)+g(i) else f(i) fi | i < k) = sum(f(i) | i < k)+sum(if p(i) f(i)+g(i) else f(i) fi | i < k) = sum(f(i) | i < k)+sum(if p(i) g(i) else 0 fi | i < k) g(i) else 0 fi | i < k) | [sum-ite] |
Thm*  f:(T f:(T  A A  T), P:(A T), P:(A   ), L:A List, s:T. list_accum(s',x'.f(s',x');s;filter(P;L)) ~ list_accum(i,y.if P(y) ), L:A List, s:T. list_accum(s',x'.f(s',x');s;filter(P;L)) ~ list_accum(i,y.if P(y) f(i,y) else i fi;s;L) f(i,y) else i fi;s;L) | [list_accum_filter] |
Thm*  P:(T P:(T   ), L2,L1:T List. list_accum(l,x.if P(x) ), L2,L1:T List. list_accum(l,x.if P(x) [x / l] else l fi;L1;L2) ~ (rev(filter(P;L2)) @ L1) [x / l] else l fi;L1;L2) ~ (rev(filter(P;L2)) @ L1) | [filter_list_accum] |
Def f91(i) == if 100 < 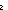 i i i-10 else f91(f91(i+11)) fi (recursive) i-10 else f91(f91(i+11)) fi (recursive) | [f91] |
Def process u j where process s i == if P(i;s) then F(i;s) else G(i;s) where xs := N(i;s); s:= H(i;s); while not null xs { s := process s (hd xs); xs := tl xs; } == if P(j;u) F(j;u) else G(j;list_accum(s',i'.process s' i' where process s i == if P(i;s) then F(i;s) else G(i;s) where xs := N(i;s); s:= H(i;s); while not null xs { s := process s (hd xs); xs := tl xs; } ;H(j;u);N(j;u))) fi (recursive) F(j;u) else G(j;list_accum(s',i'.process s' i' where process s i == if P(i;s) then F(i;s) else G(i;s) where xs := N(i;s); s:= H(i;s); while not null xs { s := process s (hd xs); xs := tl xs; } ;H(j;u);N(j;u))) fi (recursive) | [accumulate] |
Def upto(i;j) == if i < 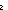 j j [i / upto(i+1;j)] else nil fi (recursive) [i / upto(i+1;j)] else nil fi (recursive) | [upto] |