| Rank | Theorem | Name |
| 6 | Thm*  L:T List, x,y:T. x before y L:T List, x,y:T. x before y  L L   ( ( A,B:T List. L = (A @ B) & (x A,B:T List. L = (A @ B) & (x  A) & (y A) & (y  B)) B)) | [l_before_decomp] |
| cites |
| 3 | Thm*  x:T, L:T List. [x / L] x:T, L:T List. [x / L] 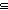 nil nil   False False | [cons_sublist_nil] |
| 1 | Thm*  x1,x2:T, L1,L2:T List. [x1 / L1] x1,x2:T, L1,L2:T List. [x1 / L1] 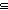 [x2 / L2] [x2 / L2]   x1 = x2 & L1 x1 = x2 & L1 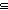 L2 L2 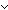 [x1 / L1] [x1 / L1] 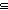 L2 L2 | [cons_sublist_cons] |
| 0 | Thm*  a,x:T. (x a,x:T. (x  [a]) [a])   x = a x = a | [member_singleton] |
| 0 | Thm*  x:T, L:T List. (x x:T, L:T List. (x  L) L)   [x] [x] 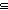 L L | [member_iff_sublist] |
| 5 | Thm*  A,B:T List, x,y:T. x before y A,B:T List, x,y:T. x before y  A @ B A @ B   x before y x before y  A A 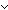 x before y x before y  B B 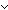 (x (x  A) & (y A) & (y  B) B) | [l_before_append_iff] |