Thm*  x:A. ( x:A. ( y:A. x = y) y:A. x = y) 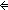  True True | [exists_explicit_2] |
Thm*  x:A. ( x:A. ( y:A. y = x) y:A. y = x) 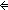  True True | [exists_explicit_1] |
Thm* ( x:A. False) x:A. False) 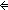  False False | [exists_false] |
Thm*  T:S, P:(T T:S, P:(T  Prop). Prop). 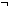 ( ( x:T. P(x)) x:T. P(x)) 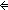  ( ( x:T. x:T. 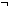 P(x)) P(x)) | [not_all] |
Thm*  T:S, P:(T T:S, P:(T  Prop). Prop). 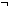 ( ( x:T. P(x)) x:T. P(x)) 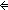  ( ( x:T. x:T. 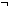 P(x)) P(x)) | [not_exists] |
Thm*  'a,'b:S, P:('b 'a,'b:S, P:('b   ), rep:('a ), rep:('a  'b), abs:('b 'b), abs:('b  'a). 'a).
Thm* iso_pair('a;'b;P;rep;abs)
Thm* 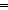 
Thm* ( rep':('a rep':('a  'b). type_definition('b;'a;P;rep')) 'b). type_definition('b;'a;P;rep')) | [type_def_iso] |
Thm*  P:(T P:(T   ). ( ). (  x:T. P(x)) x:T. P(x)) 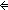  ( ( x:T. P(x)) x:T. P(x)) | [assert_of_bexists] |
Thm*  'a:S, P,Q:('a 'a:S, P,Q:('a  Prop). Prop).
Thm* ( x:'a. Q(x) x:'a. Q(x) 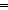  P(x)) P(x)) 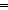  ( ( x:'a. Q(x)) x:'a. Q(x)) 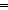  P(@x:'a. Q(x)) P(@x:'a. Q(x)) | [choose_elim_pos] |
Def type_definition('a;'b;P;rep)
Def == ( x',x'':'b. rep(x') = rep(x'') x',x'':'b. rep(x') = rep(x'')  'a 'a 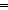  x' = x'') x' = x'')
Def == & ( x:'a. x:'a. 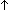 (P(x)) (P(x)) 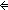  ( ( x':'b. x = rep(x'))) x':'b. x = rep(x'))) | [type_definition] |
Def   x:T. P(x) == x:T. P(x) == 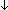  ( ( x:T. x:T. 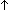 P(x)) P(x)) | [bexists] |
Def S == {T:Type|  x:T. True } x:T. True } | [stype] |