Thm*  m,n: m,n: . ndiv(m;n) . ndiv(m;n) 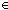  | [ndiv_wf] |
Thm*  m,n: m,n: . nmod(m;n) . nmod(m;n) 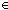  | [nmod_wf] |
Thm*  n: n: . n>0 . n>0 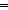 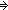 odd(n) = odd(n) = 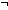 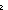 odd(n-1) odd(n-1) | [odd_pos] |
Thm*  n: n: . odd(n) . odd(n) 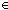 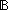 | [odd_wf] |
Thm*  n: n: . n>0 . n>0 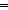 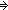 even(n) = even(n) = 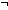 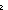 even(n-1) even(n-1) | [even_pos] |
Thm*  n: n: . even(n) . even(n) 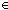 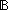 | [even_wf] |
Thm*  n: n: . n>0 . n>0 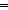 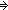 fact(n) = n fact(n) = n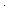 fact(n-1) fact(n-1) | [fact_pos] |
| Thm* fact(0) = 1 | [fact_zero] |
Thm*  n: n: . fact(n) . fact(n) 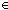  | [fact_wf] |
Thm*  m,n: m,n: . n>0 . n>0 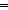 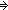 exp(m;n) = m exp(m;n) = m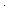 exp(m;n-1) exp(m;n-1) | [exp_pos] |
Thm*  m: m: . exp(m;0) = 1 . exp(m;0) = 1 | [exp_zero] |
Thm*  m,n: m,n: . exp(m;n) . exp(m;n) 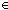  | [exp_wf] |
Thm*  m,n: m,n: . m . m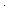 n n 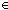  | [multiply_wf_nat] |
Thm*  m,n: m,n: . nnsub(m;n) . nnsub(m;n) 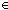  | [nnsub_wf] |
Thm*  m,n: m,n: . m . m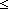 n n 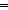 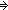 nnsub(n;m) = n-m nnsub(n;m) = n-m | [nnsub_nuprl] |
Thm*  m,n: m,n: . m+n . m+n 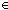  | [add_wf_nat] |
Def div ==  m: m: . .  n: n: . ndiv(m;n) . ndiv(m;n) | [hdiv] |
Def mod ==  m: m: . .  n: n: . nmod(m;n) . nmod(m;n) | [hmod] |
Def odd ==  n: n: . odd(n) . odd(n) | [hodd] |
Def even ==  n: n: . even(n) . even(n) | [heven] |
Def fact ==  n: n: . fact(n) . fact(n) | [hfact] |
Def ge ==  m: m: . .  n: n: . n . n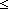 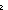 m m | [hge] |
Def le ==  m: m: . .  n: n: . m . m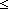 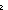 n n | [hle] |
Def gt ==  m: m: . .  n: n: . n< . n<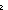 m m | [hgt] |
Def exp ==  m: m: . .  n: n: . exp(m;n) . exp(m;n) | [hexp] |
Def mult ==  m: m: . .  n: n: . m . m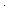 n n | [hmult] |
Def sub ==  m: m: . .  n: n: . nnsub(m;n) . nnsub(m;n) | [hsub] |
Def add ==  m: m: . .  n: n: . m+n . m+n | [hadd] |