| Rank | Theorem | Name |
| 8 | Thm*  'a:S. 'a:S.
Thm* all
Thm* ( h:'a. all h:'a. all
Thm* ( h:'a. ( h:'a. ( t:hlist('a). equal t:hlist('a). equal
Thm* ( h:'a. ( h:'a. ( t:hlist('a). (cons(h,t) t:hlist('a). (cons(h,t)
Thm* ( h:'a. ( h:'a. ( t:hlist('a). ,abs_list t:hlist('a). ,abs_list
Thm* ( h:'a. ( h:'a. ( t:hlist('a). ,(pair t:hlist('a). ,(pair
Thm* ( h:'a. ( h:'a. ( t:hlist('a). ,((( t:hlist('a). ,((( m:hnum. cond m:hnum. cond
Thm* ( h:'a. ( h:'a. ( t:hlist('a). ,((( t:hlist('a). ,((( m:hnum. (equal(m,0) m:hnum. (equal(m,0)
Thm* ( h:'a. ( h:'a. ( t:hlist('a). ,((( t:hlist('a). ,((( m:hnum. ,h m:hnum. ,h
Thm* ( h:'a. ( h:'a. ( t:hlist('a). ,((( t:hlist('a). ,((( m:hnum. ,fst(rep_list(t),pre(m)))) m:hnum. ,fst(rep_list(t),pre(m))))
Thm* ( h:'a. ( h:'a. ( t:hlist('a). ,(,suc(snd(rep_list(t)))))))) t:hlist('a). ,(,suc(snd(rep_list(t)))))))) | [hcons_def] |
| cites the following: |
| 2 | Thm*  'a,'b:S, P:('b 'a,'b:S, P:('b  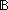 ), rep:('a ), rep:('a  'b), abs:('b 'b), abs:('b  'a), a:'a, r:'b. 'a), a:'a, r:'b.
Thm* iso_pair('a;'b;P;rep;abs) 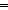 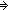 rep(a) = r rep(a) = r 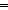 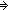 a = abs(r) a = abs(r) | [iso_pair_rep_to_abs] |
| 7 | Thm*  'a:S. iso_pair('a List;( 'a:S. iso_pair('a List;(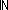   'a) 'a)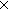 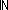 ;is_list_rep;rep_list;abs_list) ;is_list_rep;rep_list;abs_list) | [list_iso] |
| 0 | Thm*  a:T, as:T List, i: a:T, as:T List, i: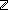 . i . i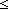 0 0 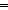 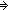 cons(a; as)[i] = a cons(a; as)[i] = a | [select_cons_hd] |
| 0 | Thm*  a:T, as:T List, i: a:T, as:T List, i: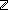 . 0<i . 0<i 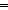 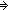 i i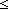 ||as|| ||as|| 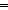 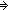 cons(a; as)[i] = as[(i-1)] cons(a; as)[i] = as[(i-1)] | [select_cons_tl] |
| 0 | Thm*  l:A List. ||l|| l:A List. ||l||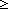 0 0 | [non_neg_length] |