Thm*  a:T, R,S:T List, b:T. [a] = (R @ (b.S)) a:T, R,S:T List, b:T. [a] = (R @ (b.S)) 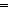  a = b a = b | [singelton_append_equals_lemma] |
Thm*  P:(T P:(T 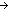 Prop), L:T List. Prop), L:T List.  x x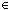 L.P(x) L.P(x)   ( ( M,N:T List, x:T. P(x) & L = (M @ (x.N))) M,N:T List, x:T. P(x) & L = (M @ (x.N))) | [list_exists_is_member_append_lemma] |
Thm*  P:(T P:(T 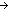 Prop), L,M:T List. Prop), L,M:T List.  x x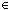 (L @ M).P(x) (L @ M).P(x)    x x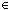 L.P(x) L.P(x) 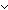  x x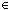 M.P(x) M.P(x) | [list_exists_append_lemma] |
Thm*  P:(T P:(T 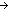 Prop), L,M:T List. Prop), L,M:T List.  x x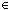 (L @ M).P(x) (L @ M).P(x)    x x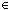 L.P(x) & L.P(x) &  x x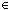 M.P(x) M.P(x) | [list_all_append_lemma] |
Thm*  L1,L2:T List, eq1,eq2,eq3:{T L1,L2:T List, eq1,eq2,eq3:{T 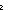 }, L3,L4:T List. Discrete{T} }, L3,L4:T List. Discrete{T} 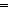  eq1 = eq2 eq1 = eq2 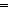  eq2 = eq3 eq2 = eq3 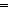  L1(~eq1)L2 L1(~eq1)L2 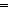  L3(~eq2)L4 L3(~eq2)L4 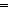  (L1 @ L3)(~eq3)(L2 @ L4) (L1 @ L3)(~eq3)(L2 @ L4) | [append_functionality_wrt_list_iso] |
Thm*  eq:{T= eq:{T=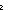 }, L:T List, x:T. x( }, L:T List, x:T. x(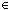 eq) L eq) L 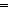  ( ( M,N:T List. L = (M @ (x.N)) & remove(eq;x;L) = (M @ N)) M,N:T List. L = (M @ (x.N)) & remove(eq;x;L) = (M @ N)) | [is_member_remove_lemma] |
Thm*  eq:{T= eq:{T=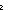 }, L:T List, x:T. ( }, L:T List, x:T. ( M,N:T List. L = (M @ (x.N))) M,N:T List. L = (M @ (x.N))) 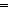  x( x(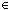 eq) L eq) L | [append_is_member_lemma] |
Thm*  L1,L2:T List, eq1,eq2,eq3:{T L1,L2:T List, eq1,eq2,eq3:{T 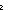 }, L3,L4:T List. Discrete{T} }, L3,L4:T List. Discrete{T} 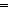  eq1 = eq2 eq1 = eq2 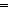  eq2 = eq3 eq2 = eq3 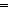  L1( L1(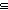 eq1)L2 eq1)L2 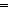  L3( L3(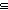 eq2)L4 eq2)L4 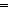  (L1 @ L3)( (L1 @ L3)(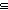 eq3)(L2 @ L4) eq3)(L2 @ L4) | [append_functionality_wrt_sublist] |
Thm* Discrete{T} 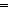  ( ( eq:{T eq:{T 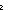 }, L,M:T List. (L @ M)(~eq)(M @ L)) }, L,M:T List. (L @ M)(~eq)(M @ L)) | [append_commutes_under_list_iso] |
Thm* Discrete{T} 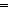  ( ( eq:{T eq:{T 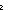 }, L,M:T List. (L @ M)( }, L,M:T List. (L @ M)(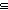 eq)(M @ L)) eq)(M @ L)) | [append_commutes_under_sublist] |
Thm*  eq:{T eq:{T 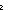 }, L,M:T List, x:T. x( }, L,M:T List, x:T. x(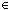 eq) (L @ M) eq) (L @ M)   x( x(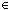 eq) (M @ L) eq) (M @ L) | [append_commutes_under_is_member] |
Thm*  eq:{T eq:{T 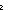 }, x:T, L,M:T List. x( }, x:T, L,M:T List. x(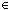 eq) (L @ M) eq) (L @ M)   x( x(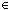 eq) L eq) L 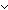 x( x(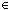 eq) M eq) M | [is_member_append_disjunction_lemma] |
Thm*  eq:{T eq:{T 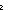 }, L,M:T List, x:T. x( }, L,M:T List, x:T. x(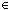 eq) (L @ M) eq) (L @ M)   x( x(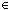 eq) L eq) L 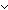 x( x(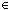 eq) M eq) M | [is_member_of_append_lemma] |
Thm*  eq:{T eq:{T 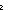 }, L:T List, x:T. x( }, L:T List, x:T. x(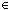 eq) L eq) L 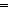  ( ( M,N:T List, y:T. eq(x,y) & L = (M @ (y.N))) M,N:T List, y:T. eq(x,y) & L = (M @ (y.N))) | [is_member_append_lemma1] |
Thm*  eq:{T= eq:{T=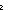 }, L:T List, x:T. x( }, L:T List, x:T. x(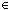 eq) L eq) L 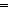  ( ( M,N:T List. L = (M @ (x.N))) M,N:T List. L = (M @ (x.N))) | [is_member_append_lemma] |
Thm*  L1,L2,L3:T List. (L1 @ (L2 @ L3)) = ((L1 @ L2) @ L3) L1,L2,L3:T List. (L1 @ (L2 @ L3)) = ((L1 @ L2) @ L3) | [append_associative] |
Thm*  L:T List. (L @ nil) = L L:T List. (L @ nil) = L | [append_nil_right_identity] |