Thm*  ds,da:Collection(dec()), de:sig(), rho:Decl, st1:Collection(SimpleType)
, e1:{1of([[de]] rho)}, s:{[[ds]] rho}, a:[[st1]] rho, tr:trace_env([[da]] rho), l:Term List.
( ds,da:Collection(dec()), de:sig(), rho:Decl, st1:Collection(SimpleType)
, e1:{1of([[de]] rho)}, s:{[[ds]] rho}, a:[[st1]] rho, tr:trace_env([[da]] rho), l:Term List.
( i: i: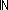 ||l||. trace_consistent(rho;da;tr.proj;l[i])) ||l||. trace_consistent(rho;da;tr.proj;l[i])) 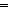 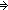 (
( ls:SimpleType List, f:reduce( ls:SimpleType List, f:reduce(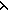 s,m. [[s]] rho s,m. [[s]] rho 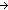 m;Prop;ls).
||ls|| = ||l|| m;Prop;ls).
||ls|| = ||l|| 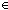 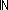 & ( & ( i: i: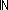 . i < ||l|| . i < ||l|| 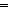 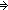 ls[i] ls[i] 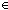 term_types(ds;st1;de;l[i])) term_types(ds;st1;de;l[i])) 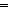 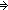 list_accum(x,t.x([[t]] e1 s a tr);f;l)
list_accum(x,t.x([[t]] e1 s a tr);f;l) 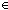 Prop) Prop) | [rel_mng_lemma] |
Thm*  ds,da:Collection(dec()), de:sig(), rho:Decl, st1:Collection(SimpleType)
, e1:{1of([[de]] rho)}, s,s':{[[ds]] rho}, a:[[st1]] rho, tr:trace_env([[da]] rho), l:Term List.
( ds,da:Collection(dec()), de:sig(), rho:Decl, st1:Collection(SimpleType)
, e1:{1of([[de]] rho)}, s,s':{[[ds]] rho}, a:[[st1]] rho, tr:trace_env([[da]] rho), l:Term List.
( i: i: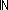 ||l||. trace_consistent(rho;da;tr.proj;l[i])) ||l||. trace_consistent(rho;da;tr.proj;l[i])) 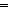 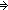 (
( ls:SimpleType List, f:reduce( ls:SimpleType List, f:reduce(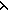 s,m. [[s]] rho s,m. [[s]] rho 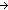 m;Prop;ls).
||ls|| = ||l|| m;Prop;ls).
||ls|| = ||l|| 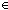 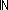 & ( & ( i: i: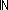 . i < ||l|| . i < ||l|| 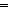 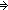 ls[i] ls[i] 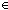 term_types(ds;st1;de;l[i])) term_types(ds;st1;de;l[i])) 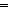 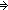 list_accum(x,t.x([[t]] e1 s s' a tr);f;l)
list_accum(x,t.x([[t]] e1 s s' a tr);f;l) 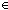 Prop) Prop) | [rel_mng_2_lemma] |
|
Def rel_mng_2(r; rho; ds; da; de; e; s; s'; a; tr)
== list_accum(x,t.x([[t]] 1of(e) s s' a tr);[[r.name]] rho 2of(e) ;r.args) | [rel_mng_2] |
|
Def [[r]] rho ds da de e s a tr
== list_accum(x,t.x([[t]] 1of(e) s a tr);[[r.name]] rho 2of(e) ;r.args) | [rel_mng] |