Thm*  da:k:Knd fp-> Type, k:{k:Knd| k da:k:Knd fp-> Type, k:{k:Knd| k  dom(da) & isrcv(k) }. dom(da) & isrcv(k) }.
Thm* da-outlink-f(da;k)  IdLnk IdLnk Id Id Type Type | [da-outlink-f_wf] |
Thm*  eq:EqDecider(A), f,g:a:A fp-> Top, x:A, z:Top. eq:EqDecider(A), f,g:a:A fp-> Top, x:A, z:Top.
Thm* f 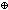 g(x)?z ~ if x g(x)?z ~ if x  dom(f) dom(f)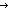 f(x)?z else g(x)?z fi f(x)?z else g(x)?z fi | [fpf-join-cap-sq] |
Thm*  B,C:(A B,C:(A  Type), eq:EqDecider(A), f:a:A fp-> B(a), g:a:A fp-> C(a), x:A. Type), eq:EqDecider(A), f:a:A fp-> B(a), g:a:A fp-> C(a), x:A.
Thm* x  dom(f) dom(f) 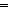 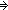 f f 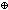 g(x) = f(x) g(x) = f(x)  B(x) B(x) | [fpf-join-ap-left] |
Thm*  B:(A B:(A  Type), eq:EqDecider(A), f,g:a:A fp-> B(a), x:A. Type), eq:EqDecider(A), f,g:a:A fp-> B(a), x:A.
Thm* x  dom(f dom(f 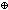 g) g) 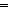 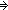 f f 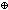 g(x) = if x g(x) = if x  dom(f) dom(f)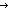 f(x) else g(x) fi f(x) else g(x) fi  B(x) B(x) | [fpf-join-ap] |
Thm*  A:Type, B:(A A:Type, B:(A  Type), f:a:A fp-> B(a), eq:EqDecider(A), x:A, Type), f:a:A fp-> B(a), eq:EqDecider(A), x:A,
Thm*  P:(a:{a:A| a P:(a:{a:A| a  dom(f) } dom(f) }  B(a) B(a)  Prop). z != f(x) ==> P(x,z) Prop). z != f(x) ==> P(x,z)  Prop Prop | [fpf-val_wf] |