| Rank | Theorem | Name |
| 4 | Thm*  R:(Id R:(Id  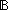 ), in,out:(|R| ), in,out:(|R|  IdLnk). IdLnk).
Thm* ring(R;in;out) 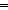  ( (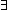 L:|R| List. 0<||L|| & ( L:|R| List. 0<||L|| & ( i:|R|. (i i:|R|. (i  L))) L))) | [ring-list] |
| cites the following: |
| 1 | Thm*  n: n: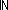 . ||upto(n)|| ~ n . ||upto(n)|| ~ n | [length_upto] |
| 0 | Thm*  f:(A f:(A  B), as:A List. ||map(f;as)|| = ||as|| B), as:A List. ||map(f;as)|| = ||as||   | [map_length] |
| 2 | Thm*  a:T List, x:T', f:(T a:T List, x:T', f:(T  T'). (x T'). (x  map(f;a)) map(f;a)) 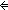  ( (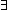 y:T. (y y:T. (y  a) & x = f(y)) a) & x = f(y)) | [member_map] |
| 0 | Thm*  n,m: n,m: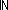 , f,i:Top. (f^n+m(i)) ~ (f^n(f^m(i))) , f,i:Top. (f^n+m(i)) ~ (f^n(f^m(i))) | [fun_exp_add_sq] |
| 3 | Thm*  n,i: n,i: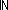 . i<n . i<n 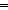  (i (i  upto(n)) upto(n)) | [member_upto2] |