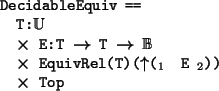Next: Messages
Up: Formal Model of Traces,
Previous: Formal Model of Traces,
The formal model of many concepts consists of a type,
operations defined over that type, and assumptions (axioms) about the operations.
We like to package the type and its operations and assumptions
into one formal object that we call a structure.
Every structure M is a tuple whose first component, which we write as |M| and call the
carrier of M, is a type, and whose other components are
functions defined over |M| or propositions about these functions.
Thus every structure is a member of the type
Structure defined as
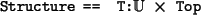
The second component type Top allows us to form subtypes of Structure by
replacing Top with other types.
For example, we define the structure of a decidable equivalence relation as follows
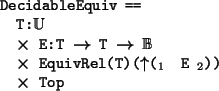
If D is a member of DecidableEquiv the the second component of D, which we
write as =
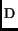 , is a binary boolean relation on |D|.
The third component is a witness that =
, is a binary boolean relation on |D|.
The third component is a witness that =
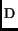 is an equivalence relation on |D|
and the final Top in the structure allows us to form subtypes of DecidableEquiv
that have additional operations or assumptions.
is an equivalence relation on |D|
and the final Top in the structure allows us to form subtypes of DecidableEquiv
that have additional operations or assumptions.



Next: Messages
Up: Formal Model of Traces,
Previous: Formal Model of Traces,
Richard Eaton
2002-02-20