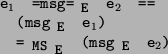Next: Trace Properties and Refinement
Up: Formal Model of Traces,
Previous: Messages
We say that E is an EventStruct if it provides a type |E| of
events, a message structure, MS
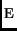 , and three functions,
msg
, and three functions,
msg
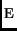 , loc
, loc
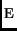 , and is-send
, and is-send
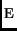 .
When is-send
.
When is-send
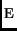 e is true we say that event e |E|
is a send event; otherwise we call it a deliver event and write is-deliver
e is true we say that event e |E|
is a send event; otherwise we call it a deliver event and write is-deliver
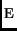 (e).
The location of event e is loc
(e).
The location of event e is loc
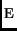 e, and its message content is msg
e, and its message content is msg
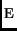 e
which is a member of |MS
e
which is a member of |MS
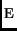 |.
Using these functions we define the binary relation, e
|.
Using these functions we define the binary relation, e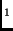 =msg=
=msg=
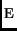 e
e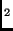 ,
that holds when events e
,
that holds when events e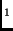 and e
and e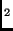 have the same message content. For example,
e
have the same message content. For example,
e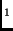 and e
and e might be delivery events of a message m at two different locations.
We can show that this relation is an equivalence relation on events.
might be delivery events of a message m at two different locations.
We can show that this relation is an equivalence relation on events.
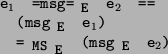
The formal definition of the type of event structures is

Given an event structure, E, a trace is just a list of events
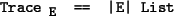
A trace tr defines an ordering of the events in it. We also call the list indices of
tr, the members of ||tr||, times and we say that event tr[k] occured at
time k.
The message in event x was delivered at time k if
![\begin{program*}
\> \\
\> x delivered at time k ==\\
\> (\muparrow{}(x =msg=$_...
...\ tr[k]))\\
\> \mwedge{} is-deliver$_{\mbox{\small {E}}}$(tr[k])
\end{program*}](img20.png)
If the message in event x was delivered at some location earlier than any delivery
of the message in event y at that same location, then
![\begin{program*}
\> \\
\> x somewhere delivered before y ==\\
\> \mexists{}k:\...
...x{\small {E}}}$\ tr[k]))\\
\> {}\mRightarrow{} (k \mleq{} k'))))
\end{program*}](img21.png)
Here is a simple lemma about this relation that we will need later.
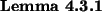

proof: If a somewhere delivered before b then there is a time k and a location,
p = (loc
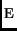 tr[k]) such that the message in event a was delivered to location p at time k
but no delivery of the message in event b to location p has occured
before time k. If a delivery of the message in event c to location p has
occured before time k, then c somewhere delivered before b. If not, then
a somewhere delivered before c. This case split is decidable, so the conclusion
follows
tr[k]) such that the message in event a was delivered to location p at time k
but no delivery of the message in event b to location p has occured
before time k. If a delivery of the message in event c to location p has
occured before time k, then c somewhere delivered before b. If not, then
a somewhere delivered before c. This case split is decidable, so the conclusion
follows



Next: Trace Properties and Refinement
Up: Formal Model of Traces,
Previous: Messages
Richard Eaton
2002-02-20
![\begin{program*}
\> \\
\> x delivered at time k ==\\
\> (\muparrow{}(x =msg=$_...
...\ tr[k]))\\
\> \mwedge{} is-deliver$_{\mbox{\small {E}}}$(tr[k])
\end{program*}](img20.png)
![\begin{program*}
\> \\
\> x somewhere delivered before y ==\\
\> \mexists{}k:\...
...x{\small {E}}}$\ tr[k]))\\
\> {}\mRightarrow{} (k \mleq{} k'))))
\end{program*}](img21.png)