Thm*  L1,L2,L:T List, x:T. L1,L2,L:T List, x:T.
Thm* no_repeats(T;L)   L1 @ [x] L1 @ [x] 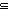 L L   [x / L2] [x / L2] 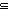 L L   L1 @ [x / L2] L1 @ [x / L2] 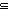 L L | [append_overlapping_sublists] |
Thm*  l1,l2,l3:T List. l1 l1,l2,l3:T List. l1  l2 l2   l1 l1  l2 @ l3 l2 @ l3 | [iseg_append] |
Thm*  P:(T P:(T 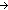 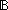 ), l1,l2:T List. filter(P;l1 @ l2) ~ (filter(P;l1) @ filter(P;l2)) ), l1,l2:T List. filter(P;l1 @ l2) ~ (filter(P;l1) @ filter(P;l2)) | [filter_append] |
Thm*  x:T, l1,l2:T List. (x x:T, l1,l2:T List. (x  l1 @ l2) l1 @ l2) 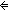  (x (x  l1) l1) 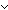 (x (x  l2) l2) | [member_append] |
Thm*  l:T List. (l @ nil) ~ l l:T List. (l @ nil) ~ l | [append_nil_sq] |
Thm*  l1,l2:T List. (l1 @ l2) = nil l1,l2:T List. (l1 @ l2) = nil 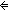  l1 = nil & l2 = nil l1 = nil & l2 = nil | [append_is_nil] |
Thm*  Q:((T List) Q:((T List) 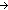 Prop). Prop).
Thm* Q(nil)   ( ( ys:T List, x:T. Q(ys) ys:T List, x:T. Q(ys)   Q(ys @ [x])) Q(ys @ [x]))   ( ( zs:T List. Q(zs)) zs:T List. Q(zs)) | [list_append_singleton_ind] |
Thm*  L:T List. 0<||L|| L:T List. 0<||L||   ( (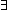 x:T, L':T List. L = (L' @ [x])) x:T, L':T List. L = (L' @ [x])) | [list_decomp_reverse] |
Thm*  f,as':Top, A:Type, as:A List. map(f;as @ as') ~ (map(f;as) @ map(f;as')) f,as':Top, A:Type, as:A List. map(f;as @ as') ~ (map(f;as) @ map(f;as')) | [map_append_sq] |
Thm*  L:T List, P:( L:T List, P:(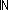 ||L|| ||L|| 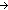 Prop). Prop).
Thm* ( x: x: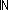 ||L||. Dec(P(x))) ||L||. Dec(P(x)))
Thm*  
Thm* ( i,j: i,j: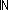 ||L||. P(i) ||L||. P(i)   i<j i<j   P(j)) P(j))
Thm*  
Thm* (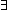 L_1,L_2:T List. L = (L_1 @ L_2) & ( L_1,L_2:T List. L = (L_1 @ L_2) & ( i: i: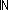 ||L||. P(i) ||L||. P(i) 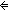  ||L_1|| ||L_1|| i)) i)) | [append_split2] |
Thm*  L:T List, n:{0...||L||}. (firstn(n;L) @ nth_tl(n;L)) = L L:T List, n:{0...||L||}. (firstn(n;L) @ nth_tl(n;L)) = L | [append_firstn_lastn] |
Def l1  l2 == l2 == 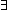 l:T List. l2 = (l1 @ l) l:T List. l2 = (l1 @ l) | [iseg] |
Def mklist(n;f) == primrec(n;nil;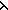 i,l. l @ [(f(i))]) i,l. l @ [(f(i))]) | [mklist] |