| Theorem | Name |
Thm*  L1,L2:T List. L1 L1,L2:T List. L1  L2 L2 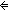  ( (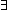 n: n: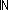 (||L2||+1). L1 = firstn(n;L2)) (||L2||+1). L1 = firstn(n;L2)) | [firstn_is_iseg] |
| cites the following: |
Thm*  as,bs:T List. ||as @ bs|| = ||as||+||bs|| as,bs:T List. ||as @ bs|| = ||as||+||bs||  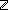 | [length_append] |
Thm*  l:T List. ||l|| = 0 l:T List. ||l|| = 0  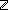 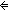  l = nil l = nil | [length_zero] |
Thm*  as:A List, n:{0...||as||}. ||firstn(n;as)|| = n as:A List, n:{0...||as||}. ||firstn(n;as)|| = n  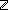 | [length_firstn] |
Thm*  L:T List, n:{0...||L||}. (firstn(n;L) @ nth_tl(n;L)) = L L:T List, n:{0...||L||}. (firstn(n;L) @ nth_tl(n;L)) = L | [append_firstn_lastn] |