Thm*  R1,R2:(T R1,R2:(T  T T  Prop). Prop).
Thm* (Sym x,y:T. x R1 y)   (Sym x,y:T. x R2 y) (Sym x,y:T. x R2 y)   (Sym x,y:T. x (R1 (Sym x,y:T. x (R1 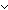 R2) y) R2) y) | [symmetric_rel_or] |
Thm*  R:(T R:(T  T T  Prop). (Sym x,y:T. x R y) Prop). (Sym x,y:T. x R y)   (Sym x,y:T. x (R^*) y) (Sym x,y:T. x (R^*) y) | [rel_star_symmetric] |
Thm*  R:(T R:(T  T T  Prop), x,y:T. (x R^*^-1 y) Prop), x,y:T. (x R^*^-1 y) 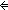  (x (R^-1^*) y) (x (R^-1^*) y) | [rel_inverse_star] |
Thm*  R:(T R:(T  T T  Prop), n: Prop), n: , x,y:T. (x R^n^-1 y) , x,y:T. (x R^n^-1 y) 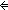  (x R^-1^n y) (x R^-1^n y) | [rel_inverse_exp] |
Thm*  x,y:T, R:(T x,y:T, R:(T  T T  Prop). x = y Prop). x = y   (x (R^*) y) (x (R^*) y) | [rel_star_weakening] |
Thm*  R:(T R:(T  T T  Prop), x,y,z:T. (x R y) Prop), x,y,z:T. (x R y)   (y (R^*) z) (y (R^*) z)   (x (R^*) z) (x (R^*) z) | [rel_star_trans] |
Thm*  R:(T R:(T  T T  Prop), x,y:T. (x R y) Prop), x,y:T. (x R y)   (x (R^*) y) (x (R^*) y) | [rel_rel_star] |
Thm*  E:(T E:(T  T T  Prop), x,y:T. EquivRel(T)(_1 E _2) Prop), x,y:T. EquivRel(T)(_1 E _2)   (x (E^*) y) (x (E^*) y)   (x E y) (x E y) | [rel_star_of_equiv] |
Thm*  R,R2:(T R,R2:(T  T T  Prop). Prop).
Thm* Trans(T)(R2(_1,_2))
Thm*  
Thm* ( x,y:T. (x R y) x,y:T. (x R y)   (x R2 y)) (x R2 y))   ( ( x,y:T. (x (R^*) y) x,y:T. (x (R^*) y)   (x R2 y) (x R2 y) 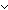 x = y) x = y) | [rel_star_closure] |
Thm*  R1,R2:(T R1,R2:(T  T T  Prop), x,y:T. R1 => R2 Prop), x,y:T. R1 => R2   (x (R1^*) y) (x (R1^*) y)   (x (R2^*) y) (x (R2^*) y) | [rel_star_monotonic] |
Thm*  R:(T R:(T  T T  Prop), x,y,z:T. (x (R^*) y) Prop), x,y,z:T. (x (R^*) y)   (y (R^*) z) (y (R^*) z)   (x (R^*) z) (x (R^*) z) | [rel_star_transitivity] |
Thm*  P:(T P:(T  Prop), R1,R2:(T Prop), R1,R2:(T  T T  Prop). Prop).
Thm* ( x,y:T. (x R1 y) x,y:T. (x R1 y)   (x R2 y)) (x R2 y))   R2 preserves P R2 preserves P   R1 preserves P R1 preserves P | [preserved_by_monotone] |
Thm*  R:(T R:(T  T T  Prop), m,n: Prop), m,n: , x,y,z:T. (x R^m y) , x,y,z:T. (x R^m y)   (y R^n z) (y R^n z)   (x R^m+n z) (x R^m+n z) | [rel_exp_add] |
Thm*  k,n: k,n: , R:( , R:( n n   n n  Prop). ( Prop). ( i,j: i,j: n. Dec(i R j)) n. Dec(i R j))   ( ( i,j: i,j: n. Dec(i R^k j)) n. Dec(i R^k j)) | [decidable__rel_exp] |
Def (R1 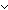 R2)(x,y) == (x R1 y) R2)(x,y) == (x R1 y) 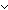 (x R2 y) (x R2 y) | [rel_or] |
| Def R^-1(x,y) == y R x | [rel_inverse] |
Def (R^*)(x,y) == 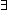 n: n: . x R^n y . x R^n y | [rel_star] |
Def R preserves P ==  x,y:T. P(x) x,y:T. P(x)   (x R y) (x R y)   P(y) P(y) | [preserved_by] |
Def R1 => R2 ==  x,y:T. (x R1 y) x,y:T. (x R1 y)   (x R2 y) (x R2 y) | [rel_implies] |
Def R^n == if n=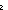 0 0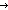 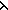 x,y. x = y x,y. x = y  T else T else 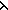 x,y. x,y. 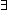 z:T. (x R z) & (z R^n-1 y) fi z:T. (x R z) & (z R^n-1 y) fi
Def (recursive) | [rel_exp] |