| | Who Cites sm all? |
|
| sm_all | Def 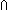 i:I
M(i)
== mk_sm(M(i).da for i i:I
M(i)
== mk_sm(M(i).da for i 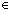 I,
M(i).ds for i I,
M(i).ds for i 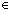 I, I,
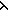 s. s. i:I. M(i).init(s), i:I. M(i).init(s),
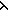 s1,a,s2. s1,a,s2.  i:I. M(i).trans(s1,a,s2)) i:I. M(i).trans(s1,a,s2)) |
|
| sm_trans |
Def t.trans == 2of(2of(2of(t))) |
| | |
Thm*  M:sm{i:l}(). M.trans M:sm{i:l}(). M.trans 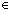 M.state M.state 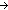 M.action M.action 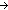 M.state M.state 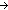 Prop Prop |
|
| sm_init |
Def t.init == 1of(2of(2of(t))) |
| | |
Thm*  M:sm{i:l}(). M.init M:sm{i:l}(). M.init 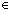 M.state M.state 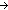 Prop Prop |
|
| sm_ds |
Def t.ds == 1of(2of(t)) |
| | |
Thm*  t:sm{i:l}(). t.ds t:sm{i:l}(). t.ds 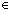 Decl Decl |
|
| dall |
Def D(i) for i 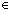 I(x) == I(x) == 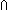 i:I. D(i)(x) i:I. D(i)(x) |
| | | Thm*  I:Type, D:(I I:Type, D:(I 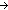 Decl). D(i) for i Decl). D(i) for i 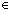 I I 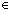 Decl Decl |
|
| sm_da |
Def t.da == 1of(t) |
| | |
Thm*  t:sm{i:l}(). t.da t:sm{i:l}(). t.da 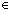 Decl Decl |
|
| mk_sm |
Def mk_sm(da, ds, init, trans) == < da,ds,init,trans > |
| | | Thm*  da,ds:Decl, init:({ds} da,ds:Decl, init:({ds} 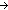 Prop), trans:({ds} Prop), trans:({ds} 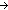 ( (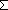 da) da) 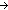 {ds} {ds} 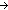 Prop).
mk_sm(da, ds, init, trans) Prop).
mk_sm(da, ds, init, trans) 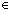 sm{i:l}() sm{i:l}() |
|
| pi2 |
Def 2of(t) == t.2 |
| | |
Thm*  A:Type, B:(A A:Type, B:(A 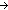 Type), p:(a:A Type), p:(a:A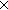 B(a)). 2of(p) B(a)). 2of(p) 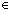 B(1of(p)) B(1of(p)) |
|
| pi1 |
Def 1of(t) == t.1 |
| | | Thm*  A:Type, B:(A A:Type, B:(A 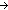 Type), p:(a:A Type), p:(a:A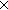 B(a)). 1of(p) B(a)). 1of(p) 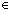 A A |