Selected Objects
| def | lang_rel | L-induced Equiv(x,y) ==  z:A*. L(z @ x) z:A*. L(z @ x)   L(z @ y) L(z @ y) |
| THM | lang_rel_refl |  L:LangOver(A). Refl(A*;x,y.x L-induced Equiv y) L:LangOver(A). Refl(A*;x,y.x L-induced Equiv y) |
| THM | lang_rel_symm |  L:LangOver(A). Sym x,y:A*. x L-induced Equiv y L:LangOver(A). Sym x,y:A*. x L-induced Equiv y |
| THM | lang_rel_tran |  L:LangOver(A). Trans x,y:A*. x L-induced Equiv y L:LangOver(A). Trans x,y:A*. x L-induced Equiv y |
| THM | lang_rel_equi |  L:LangOver(A). EquivRel x,y:A*. x L-induced Equiv y L:LangOver(A). EquivRel x,y:A*. x L-induced Equiv y |
| def | mn_quo_append | z@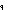 x == z @ x x == z @ x |
| THM | mn_quo_append_assoc |  R:(Alph* R:(Alph*  Alph* Alph*  Prop).
(EquivRel x,y:Alph*. x R y) Prop).
(EquivRel x,y:Alph*. x R y)   (
( x,y,z:Alph*. (x R y) x,y,z:Alph*. (x R y)   ((z @ x) R (z @ y))) ((z @ x) R (z @ y)))   (
( z1,z2:Alph*, y:x,y:Alph*//(x R y). z1 @ z2@ z1,z2:Alph*, y:x,y:Alph*//(x R y). z1 @ z2@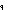 y = z1@ y = z1@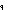 z2@ z2@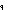 y) y) |
| def | lquo_rel | Rg(x,y) ==  z:A*. g(z@ z:A*. g(z@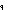 x) x)   g(z@ g(z@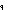 y) y) |
| THM | lquo_rel_refl |  R:(A* R:(A*  A* A*  Prop).
(EquivRel x,y:A*. x R y) Prop).
(EquivRel x,y:A*. x R y)   (
( x,y,z:A*. (x R y) x,y,z:A*. (x R y)   ((z @ x) R (z @ y))) ((z @ x) R (z @ y)))   (
( g:((x,y:A*//(x R y)) g:((x,y:A*//(x R y))   ). Refl(x,y:A*//(x R y);u,v.u Rg v)) ). Refl(x,y:A*//(x R y);u,v.u Rg v)) |
| THM | lquo_rel_symm |  R:(A* R:(A*  A* A*  Prop).
(EquivRel x,y:A*. x R y) Prop).
(EquivRel x,y:A*. x R y)   (
( x,y,z:A*. (x R y) x,y,z:A*. (x R y)   ((z @ x) R (z @ y))) ((z @ x) R (z @ y)))   (
( g:((x,y:A*//(x R y)) g:((x,y:A*//(x R y))   ). Sym u,v:x,y:A*//(x R y). u Rg v) ). Sym u,v:x,y:A*//(x R y). u Rg v) |
| THM | lquo_rel_tran |  R:(A* R:(A*  A* A*  Prop).
(EquivRel x,y:A*. x R y) Prop).
(EquivRel x,y:A*. x R y)   (
( x,y,z:A*. (x R y) x,y,z:A*. (x R y)   ((z @ x) R (z @ y))) ((z @ x) R (z @ y)))   (
( g:((x,y:A*//(x R y)) g:((x,y:A*//(x R y))   ). Trans u,v:x,y:A*//(x R y). u Rg v) ). Trans u,v:x,y:A*//(x R y). u Rg v) |
| THM | lquo_rel_equi |  R:(A* R:(A*  A* A*  Prop).
(EquivRel x,y:A*. x R y) Prop).
(EquivRel x,y:A*. x R y)   (
( x,y,z:A*. (x R y) x,y,z:A*. (x R y)   ((z @ x) R (z @ y))) ((z @ x) R (z @ y)))   (
( g:((x,y:A*//(x R y)) g:((x,y:A*//(x R y))   ). EquivRel u,v:x,y:A*//(x R y). u Rg v) ). EquivRel u,v:x,y:A*//(x R y). u Rg v) |
| THM | Rl_iff_Rg |  R:(A* R:(A*  A* A*  Prop).
(EquivRel x,y:A*. x R y) Prop).
(EquivRel x,y:A*. x R y)   (
( x,y,z:A*. (x R y) x,y,z:A*. (x R y)   ((z @ x) R (z @ y))) ((z @ x) R (z @ y)))   (
( g:((x,y:A*//(x R y)) g:((x,y:A*//(x R y))   ), L:LangOver(A).
( ), L:LangOver(A).
( l:A*. L(l) l:A*. L(l)   g(l)) g(l))   ( ( x,y:A*. (x L-induced Equiv y) x,y:A*. (x L-induced Equiv y)   (x Rg y))) (x Rg y))) |
| THM | mn_12 |  L:LangOver(Alph).
Fin(Alph) L:LangOver(Alph).
Fin(Alph)   (
( St:Type, Auto:Automata(Alph;St). Fin(St) & L = LangOf(Auto)) St:Type, Auto:Automata(Alph;St). Fin(St) & L = LangOf(Auto))   (
( R:(Alph* R:(Alph*  Alph* Alph*  Prop).
(EquivRel x,y:Alph*. x R y) c Prop).
(EquivRel x,y:Alph*. x R y) c ( ( g:((x,y:Alph*//R(x,y)) g:((x,y:Alph*//R(x,y))   ).
Fin(x,y:Alph*//R(x,y))
& ( ).
Fin(x,y:Alph*//R(x,y))
& ( l:Alph*. L(l) l:Alph*. L(l)   g(l))
& ( g(l))
& ( x,y,z:Alph*. R(x,y) x,y,z:Alph*. R(x,y)   R((z @ x),z @ y)))) R((z @ x),z @ y)))) |
| THM | mn_23_refinment |  L:LangOver(Alph), R:(Alph* L:LangOver(Alph), R:(Alph*  Alph* Alph*  Prop).
(EquivRel x,y:Alph*. x R y) Prop).
(EquivRel x,y:Alph*. x R y)   (
( g:((x,y:Alph*//(x R y)) g:((x,y:Alph*//(x R y))   ). ).  l:Alph*. L(l) l:Alph*. L(l)   g(l))
& ( g(l))
& ( x,y,z:Alph*. (x R y) x,y,z:Alph*. (x R y)   ((z @ x) R (z @ y))) ((z @ x) R (z @ y)))
  (
( x,y:Alph*. (x R y) x,y:Alph*. (x R y)   (x L-induced Equiv y)) (x L-induced Equiv y)) |
| def | beq | p =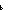 q == if p q == if p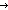 q else q else  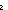 q fi q fi |
| THM | beq_id |  p: p: . p = . p =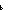 p = true p = true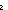 |
| THM | beq_sym |  p,q: p,q: . p = . p =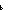 q = q = q = q =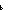 p p |
| THM | beq_eq |  p,q: p,q: . p = . p =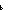 q = true q = true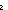   p = q p = q |
| THM | beq_neq |  p,q: p,q: . p = . p =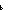 q = false q = false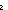    p = q p = q |
| THM | assert_iff_eq |  a,b: a,b: . (a . (a   b) b)   a = b a = b |
| THM | mn_23_lem_0 |  P:( P:(   Prop), n: Prop), n: . ( . ( k:{n...}. P(k) k:{n...}. P(k)   ( ( i: i: k. P(i))) & ( k. P(i))) & ( m: m: . P(m)) . P(m))   ( ( m: m: n. P(m)) n. P(m)) |
| THM | fin_listify | Fin(T)   ( ( TL:T*. TL:T*.  t:T. mem_f(T;t;TL)) t:T. mem_f(T;t;TL)) |
| THM | back_listify |  S:ActionSet(Alph), s:S.car.
Fin(Alph) S:ActionSet(Alph), s:S.car.
Fin(Alph)   Fin(S.car) Fin(S.car)   ( ( BL:S.car*. BL:S.car*.  t:S.car. mem_f(S.car;t;BL) t:S.car. mem_f(S.car;t;BL)   ( ( a:Alph. S.act(a,t) = s)) a:Alph. S.act(a,t) = s)) |
| THM | bool_listify |  f:(T f:(T   ). Fin(T) ). Fin(T)   ( ( fL:T*. fL:T*.  t:T. f(t) t:T. f(t)   mem_f(T;t;fL)) mem_f(T;t;fL)) |
| THM | total_back_listify |  S:ActionSet(Alph), sL:S.car*.
Fin(Alph) S:ActionSet(Alph), sL:S.car*.
Fin(Alph)   Fin(S.car)
Fin(S.car)   ( ( TBL:S.car*. TBL:S.car*.  s:S.car. mem_f(S.car;s;TBL) s:S.car. mem_f(S.car;s;TBL)   ( ( w:Alph*. mem_f(S.car;(S:w w:Alph*. mem_f(S.car;(S:w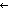 s);sL))) s);sL))) |
| THM | mn_23_lem |  R:(Alph* R:(Alph*  Alph* Alph*  Prop).
Fin(Alph) Prop).
Fin(Alph)   (EquivRel x,y:Alph*. x R y)
(EquivRel x,y:Alph*. x R y)   Fin(x,y:Alph*//(x R y))
Fin(x,y:Alph*//(x R y))   (
( x,y,z:Alph*. (x R y) x,y,z:Alph*. (x R y)   ((z @ x) R (z @ y))) ((z @ x) R (z @ y)))   (
( g:((x,y:Alph*//(x R y)) g:((x,y:Alph*//(x R y))   ), x,y:x,y:Alph*//(x R y). Dec(x Rg y)) ), x,y:x,y:Alph*//(x R y). Dec(x Rg y)) |
| THM | mn_23_lem_1 |  R:(Alph* R:(Alph*  Alph* Alph*  Prop).
Fin(Alph) Prop).
Fin(Alph)   (EquivRel x,y:Alph*. x R y)
(EquivRel x,y:Alph*. x R y)   Fin(x,y:Alph*//(x R y))
Fin(x,y:Alph*//(x R y))   (
( x,y,z:Alph*. (x R y) x,y,z:Alph*. (x R y)   ((z @ x) R (z @ y))) ((z @ x) R (z @ y)))   (
( g:((x,y:Alph*//(x R y)) g:((x,y:Alph*//(x R y))   ), x,y:x,y:Alph*//(x R y). Dec(x Rg y)) ), x,y:x,y:Alph*//(x R y). Dec(x Rg y)) |
| THM | nxn_plus_1_ge_0 |  n: n: . n . n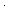 n+1 n+1 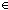  |
| THM | mn_23_Rl_equal_Rg |  L:LangOver(Alph), R:(Alph* L:LangOver(Alph), R:(Alph*  Alph* Alph*  Prop).
(EquivRel x,y:Alph*. x R y) Prop).
(EquivRel x,y:Alph*. x R y)   (
( x,y,z:Alph*. (x R y) x,y,z:Alph*. (x R y)   ((z @ x) R (z @ y))) ((z @ x) R (z @ y)))   (
( g:((x,y:Alph*//(x R y)) g:((x,y:Alph*//(x R y))   ).
( ).
( l:Alph*. L(l) l:Alph*. L(l)   g(l)) g(l))   x,y:Alph*//(x L-induced Equiv y) = x,y:Alph*//(x Rg y)) x,y:Alph*//(x L-induced Equiv y) = x,y:Alph*//(x Rg y)) |
| THM | mn_23 |  n:{1...}, A:Type, L:LangOver(A), R:(A* n:{1...}, A:Type, L:LangOver(A), R:(A*  A* A*  Prop).
Fin(A) Prop).
Fin(A)   (EquivRel x,y:A*. x R y)
(EquivRel x,y:A*. x R y)   (
( n ~ (x,y:A*//(x R y))) n ~ (x,y:A*//(x R y)))   (
( x,y,z:A*. (x R y) x,y,z:A*. (x R y)   ((z @ x) R (z @ y))) ((z @ x) R (z @ y)))   (
( g:((x,y:A*//(x R y)) g:((x,y:A*//(x R y))   ). ).  l:A*. L(l) l:A*. L(l)   g(l)) g(l))   (
( m: m: . .  m ~ (x,y:A*//(x L-induced Equiv y))) & ( m ~ (x,y:A*//(x L-induced Equiv y))) & ( l:A*. Dec(L(l))) l:A*. Dec(L(l))) |
| THM | mn_31 |  L:LangOver(Alph).
Fin(Alph) L:LangOver(Alph).
Fin(Alph)   Fin(x,y:Alph*//L-induced Equiv(x,y)) & (
Fin(x,y:Alph*//L-induced Equiv(x,y)) & ( l:Alph*. Dec(L(l))) l:Alph*. Dec(L(l)))   (
( St:Type, Auto:Automata(Alph;St). Fin(St) & L = LangOf(Auto)) St:Type, Auto:Automata(Alph;St). Fin(St) & L = LangOf(Auto)) |