Nuprl Lemma : seg_sum0
r:
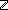. L: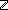 List. (seg_sum(0;r;L) = initseg_sum(r;L))
Proof
Definitions occuring in Statement :
initseg_sum: initseg_sum(r;L),
seg_sum: seg_sum(p;q;L),
list: T List,
all: x:A. B[x],
natural_number: $n,
int: ,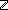
equal: s = t
Definitions :
seg_sum: seg_sum(p;q;L),
initseg_sum: initseg_sum(r;L),
segment: as[m..n
],
nth_tl: nth_tl(n;as),
le_int: i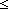 
z j,
lt_int: i <z j,
bnot: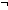 
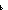b,
ifthenelse: if b then t else f fi ,
bfalse: ff,
btrue: tt,
member: t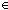 
T,
uall: [x:A]. B[x]
Lemmas :
l_sum_wf,
firstn_wf
\mforall{}r:\mBbbZ{}. \mforall{}L:\mBbbZ{} List. (seg\_sum(0;r;L) = initseg\_sum(r;L))
Date html generated:
2014_03_27-PM-01_47_18
Last ObjectModification:
2013_10_31-AM-09_25_43
Home
Index