Q 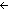
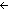
 f
f
 P == Q
P == Q 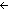

 f
f
 P
P  (
( e:{e:E| Q e} .
e:{e:E| Q e} .  e':{e:E| P e} . ((f e') = e))
e':{e:E| P e} . ((f e') = e))
Definitions :
and: P  Q,
antecedent-function: Q
Q,
antecedent-function: Q 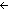

 f
f
 P,
all:
P,
all:  x:A. B[x],
exists:
x:A. B[x],
exists:  x:A. B[x],
set: {x:A| B[x]} ,
equal: s = t,
es-E: E,
apply: f a
x:A. B[x],
set: {x:A| B[x]} ,
equal: s = t,
es-E: E,
apply: f a
FDL editor aliases :
antecedent-surjection
Q \mleftarrow{}\mleftarrow{}{} f{}{} P == Q \mleftarrow{}{}{}f{}{} P \mwedge{} (\mforall{}e:\{e:E| Q e\} . \mexists{}e':\{e:E| P e\} . ((f e') = e))
Date html generated:
2010_08_27-AM-09_41_56
Last ObjectModification:
2009_12_17-PM-10_45_51
Home
Index