{ 
[A,B:Type]. [P:dataflow(A;bag(B))].
(delay-dataflow(P) 
dataflow(A;bag(B))) }
{ Proof }
Definitions occuring in Statement :
delay-dataflow: delay-dataflow(P),
dataflow: dataflow(A;B),
uall: [x:A]. B[x],
member: t T,
universe: Type
Definitions :
set: {x:A| B[x]} ,
real: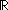 
,
grp_car: |g|,
subtype: S 
T,
int: 
,
nat: 
,
bag-size: Error :bag-size,
natural_number: $n,
lt_int: i <z j,
lambda: 
x.A[x],
so_lambda: 
x.t[x],
empty-bag: Error :empty-bag,
buffer-dataflow: buffer-dataflow(s;x.P[x]),
seq-dataflow: seq-dataflow(P;Q),
function: x:A 
B[x],
all: x:A. B[x],
bag: Error :bag,
delay-dataflow: delay-dataflow(P),
dataflow: dataflow(A;B),
equal: s = t,
axiom: Ax,
universe: Type,
uall: [x:A]. B[x],
isect: 
x:A. B[x],
member: t T
Lemmas :
dataflow_wf,
seq-dataflow_wf,
buffer-dataflow_wf,
Error :bag_wf,
lt_int_wf,
Error :bag-size_wf,
nat_wf,
Error :empty-bag_wf
\mforall{}[A,B:Type]. \mforall{}[P:dataflow(A;bag(B))]. (delay-dataflow(P) \mmember{} dataflow(A;bag(B)))
Date html generated:
2011_08_10-AM-08_17_52
Last ObjectModification:
2011_06_18-AM-08_31_27
Home
Index