{  [A:
[A: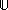 {j}].
{j}].  [B:A
[B:A 
 Type].
Type].  [x:A].
[x:A].  [v:B[x]]. (x : v
[v:B[x]]. (x : v  x:A fp-> B[x]) }
x:A fp-> B[x]) }
{ Proof }
Definitions occuring in Statement :
fpf-single: x : v,
fpf: a:A fp-> B[a],
uall:  [x:A]. B[x],
so_apply: x[s],
member: t
[x:A]. B[x],
so_apply: x[s],
member: t  T,
function: x:A
T,
function: x:A 
 B[x],
universe: Type
B[x],
universe: Type
Definitions :
uall:  [x:A]. B[x],
so_apply: x[s],
member: t
[x:A]. B[x],
so_apply: x[s],
member: t  T,
fpf: a:A fp-> B[a],
fpf-single: x : v,
and: P
T,
fpf: a:A fp-> B[a],
fpf-single: x : v,
and: P  Q,
implies: P
Q,
implies: P 
 Q,
iff: P
Q,
iff: P 

 Q,
all:
Q,
all:  x:A. B[x],
prop:
x:A. B[x],
prop: 
Lemmas :
member_singleton,
l_member_wf
\mforall{}[A:\mBbbU{}\{j\}]. \mforall{}[B:A {}\mrightarrow{} Type]. \mforall{}[x:A]. \mforall{}[v:B[x]]. (x : v \mmember{} x:A fp-> B[x])
Date html generated:
2011_08_10-AM-08_02_34
Last ObjectModification:
2011_06_18-AM-08_20_32
Home
Index