mlt_inning_test(t) ==
 s,x.
s,x.
let n,vs,i = s in
case x
of inl(inpt) => (i =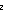 0)
0)
| inr(vote) => let m,j,v = vote in
n <z m

 ((m =
((m =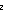 n)
n)

 (i
(i  z j
z j 
 ((j =
((j =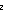 i - 1)
i - 1) 
 (||vs|| =
(||vs|| =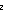 2 * t))))
2 * t))))
Definitions :
lambda:  x.A[x],
decide: case b of inl(x) => s[x] | inr(y) => t[y],
spreadn: spread3,
lt_int: i <z j,
bor: p
x.A[x],
decide: case b of inl(x) => s[x] | inr(y) => t[y],
spreadn: spread3,
lt_int: i <z j,
bor: p 
 q,
le_int: i
q,
le_int: i  z j,
band: p
z j,
band: p 
 q,
subtract: n - m,
eq_int: (i =
q,
subtract: n - m,
eq_int: (i =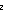 j),
length: ||as||,
multiply: n * m,
natural_number: $n
j),
length: ||as||,
multiply: n * m,
natural_number: $n
FDL editor aliases :
mlt_inning_test
mlt\_inning\_test(t) ==
\mlambda{}s,x.
let n,vs,i = s in
case x
of inl(inpt) => (i =\msubz{} 0)
| inr(vote) => let m,j,v = vote in
n <z m \mvee{}\msubb{}((m =\msubz{} n) \mwedge{}\msubb{} (i \mleq{}z j \mvee{}\msubb{}((j =\msubz{} i - 1) \mwedge{}\msubb{} (||vs|| =\msubz{} 2 * t))))
Date html generated:
2010_08_27-PM-08_30_07
Last ObjectModification:
2010_06_23-PM-11_55_21
Home
Index