---

mlt_nxt_inning() ==
  z.let s,x = z in
       let n,vs,i = s in 
      case x
      of inl(v) => <n, [], 1>
       | inr(vote) => let m,j,v = vote in 
                      if n <z m then <m, [v], j + 1>
                      if i z j then <n, [v], j + 1>
                      if (xvs.(x =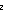 v))_b then <n, [], i + 1>
                      else <n + 1, [], 0>
                      fi 

---

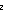Definitions :  lambda: x.A[x],  spread: spread def,  decide: case b of inl(x) => s[x] | inr(y) => t[y],  spreadn: spread3,  lt_int: i <z j,  le_int: i z j,  cons: [car / cdr],  ifthenelse: if b then t else f fi ,  bl-exists: (xL.P[x])_b,  bnot: b,  eq_int: (i = j),  add: n + m,  pair: <a, b>,  nil: [],  natural_number: $n
FDL editor aliases :  mlt_nxt_inning

---

mlt\_nxt\_inning()  ==
    \mlambda{}z.let  s,x  =  z  in
              let  n,vs,i  =  s  in 
            case  x
            of  inl(v)  =>  <n,  [],  1>
              |  inr(vote)  =>  let  m,j,v  =  vote  in 
                                            if  n  <z  m  then  <m,  [v],  j  +  1>
                                            if  i  \mleq{}z  j  then  <n,  [v],  j  +  1>
                                            if  (\mexists{}x\mmember{}vs.\mneg{}\msubb{}(x  =\msubz{}  v))\_b  then  <n,  [],  i  +  1>
                                            else  <n  +  1,  [],  0>
                                            fi 


Date html generated: 2010_08_27-PM-08_30_16
Last ObjectModification: 2010_06_23-PM-11_55_57

Home Index