{ norm-esharp-rule() 
id-fun(E#Rule) }
{ Proof }
Definitions occuring in Statement :
norm-esharp-rule: norm-esharp-rule(),
esharp-rule: E#Rule,
member: t T,
id-fun: id-fun(T)
Definitions :
norm-fst: norm-fst(N),
isect: 
x:A. B[x],
eclass: EClass(A[eo; e]),
equal: s = t,
member: t T,
function: x:A 
B[x],
all: 
x:A. B[x],
fpf: a:A fp-> B[a],
strong-subtype: strong-subtype(A;B),
set: {x:A| B[x]} ,
assert: 
b,
list: type List,
name: Name,
rec: rec(x.A[x]),
expression: Expression,
bool: 
,
Id: Id,
product: x:A 
B[x],
id-fun: id-fun(T),
implies: P 
Q,
value-type: value-type(T),
lambda: 
x.A[x],
apply: f a,
prop: 
,
so_lambda: 
x.t[x],
intensional-universe: IType,
limited-type-level: limited-type-level{i:l}(n;T),
nat: 
,
exists: 
x:A. B[x],
quotient: x,y:A//B[x; y],
tunion: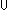 
x:A.B[x],
b-union: A 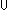B,
union: left + right,
atom: Atom,
tag-by: zT,
or: P 
Q,
rev_implies: P 
Q,
and: P 
Q,
iff: P Q,
ldag: LabeledDAG(T),
labeled-graph: LabeledGraph(T),
record: record(x.T[x]),
isect2: T1 T2,
record+: record+,
fset: FSet{T},
top: Top,
true: True,
type-monotone: Monotone(T.F[T]),
norm-snd: norm-snd(N),
sq-id-fun: sq-id-fun(T),
norm-pair: norm-pair(Na;Nb),
norm-esharp-rule: norm-esharp-rule(),
esharp-rule: E#Rule,
subtype: S 
T,
es-E-interface: E(X),
fpf-sub: f g,
fpf-cap: f(x)?z,
deq: EqDecider(T),
ma-state: State(ds),
class-program: ClassProgram(T),
universe: Type,
limited-type: LimitedType,
subtype_rel: A r B,
atom: Atom$n,
int: 
,
squash: 
T,
mkid: "$x"
Lemmas :
norm-fst_wf,
squash_wf,
subtype-value-type,
norm-pair_wf,
norm-snd_wf,
type-monotone_wf,
subtype_rel_sum,
subtype_rel_simple_product,
subtype_rel_wf,
expression_wf,
name_wf,
function-value-type,
union-value-type,
bunion-value-type,
tunion-value-type,
set-value-type,
quotient-value-type,
rec-value-type,
equal-value-type,
type-value-type,
intensional-universe_wf2,
nat_wf,
limited-type-level_wf,
intensional-universe_wf,
list-value-type,
product-value-type,
limited-type_wf,
value-type_wf,
assert_wf,
Id_wf,
id-fun_wf,
member_wf,
bool_wf
norm-esharp-rule() \mmember{} id-fun(E\#Rule)
Date html generated:
2011_08_17-PM-04_35_54
Last ObjectModification:
2010_09_21-PM-01_19_47
Home
Index