{ 
[A:Type]. [P:A 
]. [B:A 
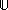{j}].
(a:{a:A| P[a]} fp-> B[a] 
r a:A fp-> B[a]) }
{ Proof }
Definitions occuring in Statement :
fpf: a:A fp-> B[a],
subtype_rel: A r B,
uall: [x:A]. B[x],
prop: ,
so_apply: x[s],
set: {x:A| B[x]} ,
function: x:A B[x],
universe: Type
Definitions :
uall: [x:A]. B[x],
prop: ,
fpf: a:A fp-> B[a],
so_apply: x[s],
member: t 
T,
all: x:A. B[x],
subtype: S T,
implies: P 
Q,
and: P 
Q,
squash: 
T,
true: True,
l_member: (x l),
exists: 
x:A. B[x],
cand: A c B,
false: False,
nat: 
,
length: ||as||,
select: l[i],
ycomb: Y,
or: P 
Q,
iff: P 
Q,
uimplies: b supposing a,
not: 
A
Lemmas :
l_member_wf,
cons_member,
length_wf1,
select_wf
\mforall{}[A:Type]. \mforall{}[P:A {}\mrightarrow{} \mBbbP{}]. \mforall{}[B:A {}\mrightarrow{} \mBbbU{}\{j\}]. (a:\{a:A| P[a]\} fp-> B[a] \msubseteq{}r a:A fp-> B[a])
Date html generated:
2011_08_10-AM-07_54_26
Last ObjectModification:
2011_06_18-AM-08_14_58
Home
Index