Step
*
of Lemma
aa_ltree-induction
 [T:Type].
[T:Type].  [P:aa_ltree(T)
[P:aa_ltree(T) 
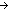
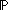 ].
].
(P[aa_lt_leaf()]

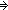 (
( val:T.
val:T.  left_subtree,right_subtree:aa_ltree(T).
left_subtree,right_subtree:aa_ltree(T).
(P[left_subtree] 
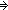 P[right_subtree]
P[right_subtree] 
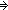 P[aa_lt_node(val;left_subtree;right_subtree)]))
P[aa_lt_node(val;left_subtree;right_subtree)]))

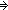 {
{ x:aa_ltree(T). P[x]})
x:aa_ltree(T). P[x]})
BY
{ DatatypeInductionAux ``aa_ltree aa_lt_leaf aa_lt_node`` }
\mforall{}[T:Type]. \mforall{}[P:aa\_ltree(T) {}\mrightarrow{} \mBbbP{}].
(P[aa\_lt\_leaf()]
{}\mRightarrow{} (\mforall{}val:T. \mforall{}left$_{subtree}$,right$_{subtree}$:aa\_ltree(T\000C).
(P[left$_{subtree}$] {}\mRightarrow{} P[right$_{subtree}$] {}\mRightarrow{} P[aa\000C\_lt\_node(val;left$_{subtree}$;right$_{subtree}$)]))
{}\mRightarrow{} \{\mforall{}x:aa\_ltree(T). P[x]\})
By
DatatypeInductionAux ``aa\_ltree aa\_lt\_leaf aa\_lt\_node``
Home
Index