---

Step * 2 2 1 of Lemma not_base_decidble_eq_diag2


1. t1,t2:Base.  Dec(t1 = t2)@i
2. eqd : B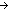ase  Base  
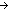
3. t1,t2:Base. 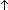 ((eqd t1 t2)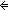  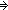t1 = t2)
4. isBot : Base  
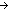
5. t:Base. (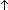(isBot t)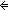  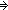t = bottom())
6. isBot fix((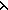t.if isBot t then 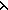x.x else bottom() fi ))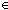  
 False
BY
{ (Assert isBot fix((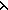t.if isBot t then 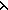x.x else bottom() fi )) 
         = isBot if isBot fix((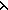t.if isBot t then 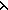x.x else bottom() fi )) then x.x else bottom() fi  BY
         (RW (AddrC [2;2] UnrollRecursionC) 0 THEN Reduce 0 THEN MaAuto)) }

1
1. t1,t2:Base.  Dec(t1 = t2)@i
2. eqd : B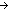ase  Base  
3. t1,t2:Base. 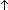 ((eqd t1 t2)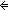  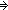t1 = t2)
4. isBot : Base  
5. t:Base. ((isBot t)  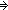t = bottom())
6. isBot fix((t.if isBot t then 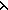x.x else bottom() fi ))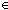  
7. isBot fix((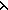t.if isBot t then 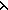x.x else bottom() fi )) 
= isBot if isBot fix((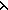t.if isBot t then 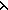x.x else bottom() fi )) then 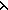x.x else bottom() fi 
 False



1.  \mforall{}t1,t2:Base.    Dec(t1  =  t2)@i
2.  eqd  :  Base  {}\mrightarrow{}  Base  {}\mrightarrow{}  \mBbbB{}
3.  \mforall{}t1,t2:Base.    (\muparrow{}(eqd  t1  t2)  \mLeftarrow{}{}\mRightarrow{}  t1  =  t2)
4.  isBot  :  Base  {}\mrightarrow{}  \mBbbB{}
5.  \mforall{}t:Base.  (\muparrow{}(isBot  t)  \mLeftarrow{}{}\mRightarrow{}  t  =  bottom())
6.  isBot  fix((\mlambda{}t.if  isBot  t  then  \mlambda{}x.x  else  bottom()  fi  ))  \mmember{}  \mBbbB{}
\mvdash{}  False


By

(Assert  isBot  fix((\mlambda{}t.if  isBot  t  then  \mlambda{}x.x  else  bottom()  fi  )) 
              =  isBot 
                  if  isBot  fix((\mlambda{}t.if  isBot  t  then  \mlambda{}x.x  else  bottom()  fi  ))  then  \mlambda{}x.x  else  bottom()  fi    BY
              (RW  (AddrC  [2;2]  UnrollRecursionC)  0  THEN  Reduce  0  THEN  MaAuto))\mcdot{}



Home Index