Step
*
1
of Lemma
not_total_enumerable_inc
1. f : 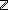

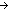
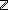

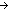
 @i
@i
2.  b:
b: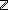

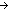
 .
. 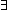 a:
a: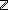 . ((f a) = b)@i
. ((f a) = b)@i
 False
False
BY
{ Assert 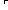
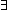 d:
d: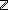

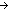
 .
.  n:
n: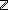 . (
. (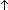 (d (n + 1))
(d (n + 1)) 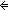

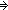
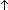
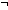
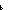 (f n (n + 1)))
(f n (n + 1)))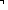
 }
}
1
.....assertion.....
1. f : 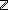

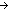
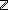

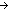
 @i
@i
2.  b:
b: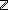

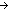
 .
. 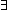 a:
a: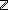 . ((f a) = b)@i
. ((f a) = b)@i

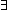 d:
d: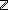

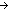
 .
.  n:
n: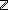 . (
. (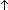 (d (n + 1))
(d (n + 1)) 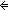

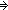
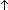
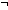
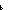 (f n (n + 1)))
(f n (n + 1)))
2
1. f : 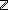

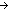
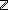

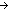
 @i
@i
2.  b:
b: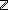

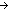
 .
. 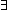 a:
a: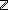 . ((f a) = b)@i
. ((f a) = b)@i
3. 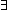 d:
d: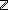

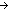
 .
.  n:
n: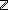 . (
. (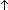 (d (n + 1))
(d (n + 1)) 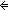

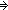
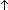
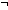
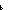 (f n (n + 1)))
(f n (n + 1)))
 False
False
1. f : \mBbbZ{} {}\mrightarrow{} \mBbbZ{} {}\mrightarrow{} \mBbbB{}@i
2. \mforall{}b:\mBbbZ{} {}\mrightarrow{} \mBbbB{}. \mexists{}a:\mBbbZ{}. ((f a) = b)@i
\mvdash{} False
By
Assert \mkleeneopen{}\mexists{}d:\mBbbZ{} {}\mrightarrow{} \mBbbB{}. \mforall{}n:\mBbbZ{}. (\muparrow{}(d (n + 1)) \mLeftarrow{}{}\mRightarrow{} \muparrow{}\mneg{}\msubb{}(f n (n + 1)))\mkleeneclose{}\mcdot{}
Home
Index