| Rank | Theorem | Name |
| 15 | Thm*  n:{1...}. n:{1...}. 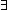 f:(Prime f:(Prime    ). f is a factorization of n ). f is a factorization of n | [prime_factorization_exists2] |
| cites the following: |
| 14 | Thm*  n:{1...}. n:{1...}.
Thm* 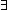 h:({2..(n+1) h:({2..(n+1) } }   ). ).
Thm* n =   {2..n+1 {2..n+1 }(h) & is_prime_factorization(2; (n+1); h) }(h) & is_prime_factorization(2; (n+1); h) | [prime_factorization_exists] |
| 0 | Thm*  a,b: a,b: , f:({a..b , f:({a..b } }   ), x: ), x: . .
Thm* 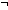 a a 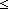 x < b x < b   complete_intseg_mset(a; b; f)(x) = 0 complete_intseg_mset(a; b; f)(x) = 0 | [complete_intseg_mset_ismin] |
| 0 | Thm*  f:(Prime f:(Prime    ), x:Prime ), x:Prime . prime_mset_complete(f)(x) = f(x) . prime_mset_complete(f)(x) = f(x) | [prime_mset_complete_isext] |
| 0 | Thm*  a,b: a,b: , f:({a..b , f:({a..b } }   ), x:{a..b ), x:{a..b }. complete_intseg_mset(a; b; f)(x) = f(x) }. complete_intseg_mset(a; b; f)(x) = f(x) | [complete_intseg_mset_isext] |
| 0 | Thm*  f:(Prime f:(Prime    ), x: ), x: . . 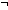 prime(x) prime(x)   prime_mset_complete(f)(x) = 0 prime_mset_complete(f)(x) = 0 | [prime_mset_complete_ismin] |