Selected Objects
| THM | extend_intseg_upperpart_down
|
 a,b: a,b: , P:({a..b , P:({a..b } }  Prop), n:{(a+1)..(b+1) Prop), n:{(a+1)..(b+1) }. }.
P(n-1)   ( ( i:{a..b i:{a..b }. n }. n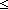 i i   P(i)) P(i))   ( ( i:{a..b i:{a..b }. n-1 }. n-1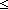 i i   P(i)) P(i)) |
| def | prime_mset_complete
|
prime_mset_complete(f)(x) == if is_prime(x)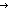 f(x) else 0 fi f(x) else 0 fi |
| THM | prime_mset_complete_isext
|
 f:(Prime f:(Prime    ), x:Prime ), x:Prime . prime_mset_complete(f)(x) = f(x) . prime_mset_complete(f)(x) = f(x) |
| THM | prime_mset_complete_ismin
|
 f:(Prime f:(Prime    ), x: ), x: . . 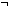 prime(x) prime(x)   prime_mset_complete(f)(x) = 0 prime_mset_complete(f)(x) = 0 |
| def | eval_factorization
|
The number of which an integer multiset is a factorization
  {a..b {a..b }(f) == }(f) ==  i:{a..b i:{a..b }. i }. i f(i) f(i) |
| THM | eval_factorization_split_mid
|
 a,c,b: a,c,b: , f:({a..b , f:({a..b } }   ). a ). a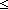 c c   c c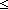 b b     {a..b {a..b }(f) = }(f) =   {a..c {a..c }(f) }(f)   {c..b {c..b }(f) }(f) |
| def | prime_factorization_of
|
f is a factorization of k
== ( x:Prime x:Prime . k<x . k<x   f(x) = 0) & k = f(x) = 0) & k =   {2..k+1 {2..k+1 }(prime_mset_complete(f)) }(prime_mset_complete(f)) |
| THM | prime_factorization_limit
|
 n: n: , f,g:(Prime , f,g:(Prime    ). ).
f is a factorization of n
 
g is a factorization of n
 
( x:{2..(n+1) x:{2..(n+1) }. prime_mset_complete(f)(x) = prime_mset_complete(g)(x)) }. prime_mset_complete(f)(x) = prime_mset_complete(g)(x))   f = g f = g |
| THM | eval_factorization_split_pluck
|
 a,c,b: a,c,b: , f:({a..b , f:({a..b } }   ). ).
a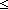 c c   c<b c<b     {a..b {a..b }(f) = }(f) =   {a..c {a..c }(f) }(f) c c f(c) f(c)   {c+1..b {c+1..b }(f) }(f) |
| def | trivial_factorization
|
trivial_factorization(z)(i) == if i=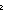 z z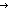 1 else 0 fi 1 else 0 fi |
| THM | trivial_factorization_comp1
|
 x,y: x,y: . x = y . x = y   trivial_factorization(x)(y) = 1 trivial_factorization(x)(y) = 1 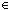  |
| THM | trivial_factorization_comp2
|
 x,y: x,y: . x . x 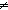 y y   trivial_factorization(x)(y) = 0 trivial_factorization(x)(y) = 0 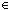  |
| THM | eval_trivial_factorization
|
 a,b: a,b: , j:{a..b , j:{a..b }. }.   {a..b {a..b }(trivial_factorization(j)) = j }(trivial_factorization(j)) = j |
| def | reduce_factorization
|
Removing one member from a factorization multiset
reduce_factorization(f; j)(i) == if i=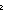 j j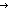 f(i)-1 else f(i) fi f(i)-1 else f(i) fi |
| THM | reduce_factorization_cancel
|
 a,b: a,b: , f,g:({a..b , f,g:({a..b } }   ), j:{a..b ), j:{a..b }. }.
0<f(j)
 
0<g(j)   reduce_factorization(f; j) = reduce_factorization(g; j) reduce_factorization(f; j) = reduce_factorization(g; j)   f = g f = g |
| THM | reduce_factorization_bound
|
 a,b: a,b: , f:({a..b , f:({a..b } }   ), j:{a..b ), j:{a..b }. }.
0<f(j)   ( ( i:{a..b i:{a..b }. reduce_factorization(f; j)(i) }. reduce_factorization(f; j)(i)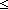 f(i)) f(i)) |
| THM | eval_factorization_nat_plus
|
 a: a: 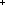 , b: , b: , f:({a..b , f:({a..b } }   ). ).   {a..b {a..b }(f) }(f) 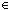  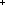 |
| THM | only_positives_prime_fed
|
 f:(Prime f:(Prime    ), n: ), n: . f is a factorization of n . f is a factorization of n   0<n 0<n |
| THM | eval_factorization_one
|
 a:{2...}, b: a:{2...}, b: , f:({a..b , f:({a..b } }   ). ).   {a..b {a..b }(f) = 1 }(f) = 1 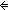  ( ( i:{a..b i:{a..b }. f(i) = 0) }. f(i) = 0) |
| THM | only_one_factored_by
|
 f:(Prime f:(Prime    ), n,n': ), n,n': . .
f is a factorization of n   f is a factorization of n' f is a factorization of n'   n = n' n = n' |
| THM | eval_factorization_one_b
|
 a:{2...}, b: a:{2...}, b: , f:({a..b , f:({a..b } }   ). ).   {a..b {a..b }(f) = 1 }(f) = 1 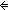  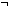 ( (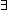 i:{a..b i:{a..b }. 0<f(i)) }. 0<f(i)) |
| THM | eval_factorization_one_c
|
 a:{2...}, b: a:{2...}, b: , f:({a..b , f:({a..b } }   ). ).   {a..b {a..b }(f) = 1 }(f) = 1 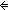  f = ( f = (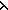 x.0) x.0) |
| THM | eval_factorization_not_one
|
 a:{2...}, b: a:{2...}, b: , f:({a..b , f:({a..b } }   ). ). 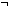   {a..b {a..b }(f) = 1 }(f) = 1 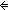  ( (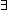 i:{a..b i:{a..b }. }. 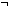 f(i) = 0) f(i) = 0) |
| THM | eval_factorization_prod
|
The pairwise sum of factorizations of a couple of numbers factorizes their product.
 a,b: a,b: , f,g:({a..b , f,g:({a..b } }   ). ).   {a..b {a..b }(f) }(f)   {a..b {a..b }(g) = }(g) =   {a..b {a..b }( }(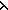 i.f(i)+g(i)) i.f(i)+g(i)) |
| THM | eval_factorization_pluck
|
 a,b: a,b: , f:({a..b , f:({a..b } }   ), z:{a..b ), z:{a..b }. }.
0<f(z)     {a..b {a..b }(f) = z }(f) = z   {a..b {a..b }(reduce_factorization(f; z)) }(reduce_factorization(f; z)) |
| THM | eval_reduce_factorization_less
|
 a: a: 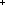 , b: , b: , f:({a..b , f:({a..b } }   ), j:{a..b ), j:{a..b }. }.
2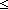 j j   0<f(j) 0<f(j)     {a..b {a..b }(reduce_factorization(f; j))< }(reduce_factorization(f; j))<  {a..b {a..b }(f) }(f) |
| THM | eval_factorization_intseg_null
|
 a,b: a,b: , f:({a..b , f:({a..b } }   ). b ). b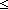 a a     {a..b {a..b }(f) = 1 }(f) = 1 |
| THM | eval_factorization_nullnorm
|
 a,b: a,b: , f:({a..b , f:({a..b } }   ). b ). b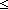 a a     {a..b {a..b }(f) = }(f) =   {a..a {a..a }(f) }(f) |
| def | is_prime_factorization
|
Prime factorization as a multiset on an interval.
is_prime_factorization(a; b; f) ==  i:{a..b i:{a..b }. 0<f(i) }. 0<f(i)   prime(i) prime(i) |
| THM | prime_mset_c_is_prime_f
|
 f:(Prime f:(Prime    ), b: ), b: . is_prime_factorization(2; b; prime_mset_complete(f)) . is_prime_factorization(2; b; prime_mset_complete(f)) |
| THM | sq_stable__is_prime_factorization
|
 a,b: a,b: , f:({a..b , f:({a..b } }   ). SqStable(is_prime_factorization(a; b; f)) ). SqStable(is_prime_factorization(a; b; f)) |
| THM | reduce_fac_pres_isprimefac
|
 a,b: a,b: , f:({a..b , f:({a..b } }   ), j:{a..b ), j:{a..b }. }.
0<f(j)
 
is_prime_factorization(a; b; f)
 
is_prime_factorization(a; b; reduce_factorization(f; j)) |
| THM | factor_divides_evalfactorization
|
 a,b: a,b: , f:({a..b , f:({a..b } }   ), j:{a..b ), j:{a..b }. 0<f(j) }. 0<f(j)   j | j |   {a..b {a..b }(f) }(f) |
| THM | nat_prime_div_each_factorLEMMA
|
 X: X: . .
prime(X)
 
( X1: X1: . X1<X . X1<X   prime(X1) prime(X1)   ( ( a,b: a,b: . X1 | a . X1 | a b b   X1 | a X1 | a 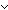 X1 | b)) X1 | b))
 
( W: W: . 0<W . 0<W   W<X W<X   ( ( t: t: . X | t . X | t W W   X | t)) X | t)) |
| THM | nat_prime_div_each_factor
|
 X: X: . prime(X) . prime(X)   ( ( a,b: a,b: . X | a . X | a b b   X | a X | a 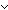 X | b) X | b) |
| THM | prime_divs_mul_via_intseg
|
 p: p: . .
prime(p)
 
( a,b: a,b: , e:({a..b , e:({a..b } }   ). ).
(a<b   p | ( p | ( i:{a..b i:{a..b }. e(i)) }. e(i))   ( (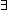 i:{a..b i:{a..b }. p | e(i))) }. p | e(i))) |
| THM | prime_divs_exp
|
 p: p: . prime(p) . prime(p)   ( ( b,z: b,z: . p | z . p | z b b   b b 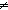 0 & p | z) 0 & p | z) |
| THM | prime_factorization_includes_prime_divisors
|
 a: a: , b: , b: , f:({a..b , f:({a..b } }   ), p: ), p: . .
is_prime_factorization(a; b; f)
 
prime(p)   p | p |   {a..b {a..b }(f) }(f)   p p 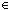 {a..b {a..b } & 0<f(p) } & 0<f(p) |
| THM | remove_prime_factor
|
 a: a: , b: , b: , f:({a..b , f:({a..b } }   ), p: ), p: . .
is_prime_factorization(a; b; f)
 
prime(p)
 
p |   {a..b {a..b }(f) }(f)     {a..b {a..b }(f) = p }(f) = p   {a..b {a..b }(reduce_factorization(f; p)) }(reduce_factorization(f; p)) |
| THM | prime_factorization_unique
|
There is at most one prime factorization of any natural number (given a range of integers to include).
 a:{2...}, b: a:{2...}, b: , g,h:({a..b , g,h:({a..b } }   ). ).
is_prime_factorization(a; b; g)
 
is_prime_factorization(a; b; h)     {a..b {a..b }(g) = }(g) =   {a..b {a..b }(h) }(h)   g = h g = h |
| def | split_factor2
|
(eliminating the power of a composite of two number by adding it to the power of its two factors)
split_factor2(g; x; y)(u)
== if u=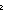 x x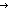 g(x)+g(x g(x)+g(x y) ; u= y) ; u=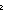 y y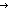 g(y)+g(x g(y)+g(x y) ; u= y) ; u=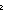 x x y y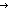 0 else g(u) fi 0 else g(u) fi |
| THM | split_factor2_char
|
Redistributing the power of a composite of two numbers in a factorization down to the factors produces another factorization of the same number, zeroing the power of the composite and leaving the powers of larger factors untouched.
 k:{2...}, g:({2..k k:{2...}, g:({2..k } }   ), x,y:{2..k ), x,y:{2..k }. }.
x y<k y<k
 
x<y
 
  {2..k {2..k }(g) = }(g) =   {2..k {2..k }(split_factor2(g; x; y)) }(split_factor2(g; x; y))
& split_factor2(g; x; y)(x y) = 0 y) = 0
& ( u:{2..k u:{2..k }. x }. x y<u y<u   split_factor2(g; x; y)(u) = g(u)) split_factor2(g; x; y)(u) = g(u)) |
| def | split_factor1
|
split_factor1(g; x)(u) == if u=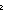 x x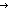 g(x)+g(x g(x)+g(x x)+g(x x)+g(x x) ; u= x) ; u=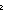 x x x x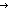 0 else g(u) fi 0 else g(u) fi |
| THM | split_factor1_char
|
Redistributing the power of a composite square in a factorization down to the square root produces another factorization of the same number, zeroing the power of the composite and leaving the powers of larger factors untouched.
 k:{2...}, g:({2..k k:{2...}, g:({2..k } }   ), x:{2..k ), x:{2..k }. }.
x x<k x<k
 
  {2..k {2..k }(g) = }(g) =   {2..k {2..k }(split_factor1(g; x)) }(split_factor1(g; x))
& split_factor1(g; x)(x x) = 0 x) = 0
& ( u:{2..k u:{2..k }. x }. x x<u x<u   split_factor1(g; x)(u) = g(u)) split_factor1(g; x)(u) = g(u)) |
| THM | can_reduce_composite_factor
|
A composite factor in a factorization can be reduced to power zero, leaving all larger factors' powers unchanged.
 k:{2...}, g:({2..k k:{2...}, g:({2..k } }   ), x,y:{2..k ), x,y:{2..k }. }.
x y<k y<k
 
(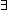 h:({2..k h:({2..k } }   ). ).
(  {2..k {2..k }(g) = }(g) =   {2..k {2..k }(h) & h(x }(h) & h(x y) = 0 & ( y) = 0 & ( u:{2..k u:{2..k }. x }. x y<u y<u   h(u) = g(u))) h(u) = g(u))) |
| THM | can_reduce_composite_factor2
|
 k:{2...}, g:({2..k k:{2...}, g:({2..k } }   ), z:{2..k ), z:{2..k }. }.
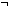 prime(z) prime(z)
 
(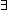 g':({2..k g':({2..k } }   ). ).
(  {2..k {2..k }(g) = }(g) =   {2..k {2..k }(g') & g'(z) = 0 & ( }(g') & g'(z) = 0 & ( u:{2..k u:{2..k }. z<u }. z<u   g'(u) = g(u))) g'(u) = g(u))) |
| THM | prime_factorization_existsLEMMA
|
 k:{2...}, n: k:{2...}, n: , g:({2..k , g:({2..k } }   ). ).
2 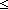 n < k+1 n < k+1
 
( i:{2..k i:{2..k }. n }. n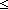 i i   0<g(i) 0<g(i)   prime(i)) prime(i))
 
(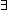 h:({2..k h:({2..k } }   ). ).   {2..k {2..k }(g) = }(g) =   {2..k {2..k }(h) & is_prime_factorization(2; k; h)) }(h) & is_prime_factorization(2; k; h)) |
| THM | prime_factorization_exists
|
 n:{1...}. n:{1...}.
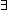 h:({2..(n+1) h:({2..(n+1) } }   ). n = ). n =   {2..n+1 {2..n+1 }(h) & is_prime_factorization(2; (n+1); h) }(h) & is_prime_factorization(2; (n+1); h) |
| def | lelt_int
|
i 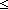 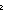 j < j <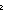 k == (i k == (i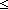 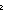 j) j)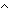 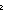 (j< (j<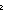 k) k) |
| THM | lelt_int_vs_lelt
|
 i,j,k: i,j,k: . i . i 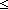 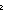 j < j <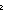 k k   i i 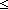 j < k j < k |
| def | complete_intseg_mset
|
complete_intseg_mset(a; b; f)(x) == if a 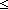 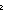 x < x <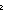 b b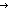 f(x) else 0 fi f(x) else 0 fi |
| THM | complete_intseg_mset_ismin
|
 a,b: a,b: , f:({a..b , f:({a..b } }   ), x: ), x: . . 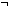 a a 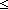 x < b x < b   complete_intseg_mset(a; b; f)(x) = 0 complete_intseg_mset(a; b; f)(x) = 0 |
| THM | complete_intseg_mset_isext
|
 a,b: a,b: , f:({a..b , f:({a..b } }   ), x:{a..b ), x:{a..b }. complete_intseg_mset(a; b; f)(x) = f(x) }. complete_intseg_mset(a; b; f)(x) = f(x) |
| THM | prime_factorization_exists2
|
Every positive integer can be factored into primes.
 n:{1...}. n:{1...}. 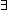 f:(Prime f:(Prime    ). f is a factorization of n ). f is a factorization of n |
| THM | prime_factorization_mset_unique
|
There is at most one prime factorization of any natural number.
 n: n: , f,g:(Prime , f,g:(Prime    ). ).
f is a factorization of n   g is a factorization of n g is a factorization of n   f = g f = g |
| THM | fta_mset
|
The Fundamental Theorem of Arithmetic (FTA)
There is a unique prime factorization for every positive integer.
 n:{1...}. n:{1...}. 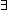 !f:(Prime !f:(Prime    ). f is a factorization of n ). f is a factorization of n |