Thm*  n:, f,g:({1...n}Peg).
Thm*  f(n) = g(n)
Thm*  
Thm*  (a:, z:{a...}.
Thm*  ((s:({a...z}{1...n-1}Peg). 
Thm*  ((s is a Hanoi(n-1 disk) seq on a..z
Thm*  ((& s(a) = f  {1...n-1}Peg
Thm*  ((& s(z) = g  {1...n-1}Peg)
Thm*  (
Thm*  ((s:({a...z}{1...n}Peg). 
Thm*  ((s is a Hanoi(n disk) seq on a..z & s(a) = f & s(z) = g))

The idea is to just add the large disk to one of the pegs, and leave it there, throughout all the stacking situations of s  {a...z}{1...n-1}Peg.

More generally, we can add any number of larger disks throughout a Hanoi sequence and it stays a Hanoi sequence. See Deepening for a discussion of this operation, s(?) {to n}  h {to n'}. Deepening a Hanoi sequence produces a Hanoi sequence:

Thm*  a,z:, n:, s:({a...z}{1...n}Peg), n':.
Thm*  nn'
Thm*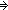  
Thm*  (h:({n+1...n'}Peg). 
Thm*  (s is a Hanoi(n disk) seq on a..z
Thm*  (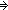
Thm*  ((s(?) {to n}  h {to n'}) is a Hanoi(n' disk) seq on a..z)

and we shall apply this lemma in our proof. Assume

(A) f(n) = g(n)

(B) s is a Hanoi(n-1 disk) seq on a..z

(C) s(a) = f  {1...n-1}Peg

(D) s(z) = g  {1...n-1}Peg

Applying the above sequence deepening lemma with n-1 for n, n for n', and i.f(n) for h gives us

(s(?) {to n-1} 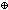 i.f(n) {to n}) is a Hanoi(n disk) seq on a..z

because of (B). To finish our proof we just need to show that for x  {1...n}

(E) (s(?) {to n-1}  i.f(n) {to n})(a,x) = f(x)  Peg

and

(F) (s(?) {to n-1}  i.f(n) {to n})(z,x) = g(x)  Peg

and for each of these two goals, we branch on whether x<n. For x<n, (E) and (F) reduce to s(a,x) = f(x) and s(z,x) = g(x), because of

Thm*  a,z:, n:, s:({a...z}{1...n}Peg), n':.
Thm*  nn'
Thm*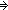  
Thm*  (h:({n+1...n'}Peg), i:{1...n'}.
Thm*  (in  (x:{a...z}. (s(?) {to n}  h {to n'})(x,i) = s(x,i)))

and follow from (C) and (D). For x = n, (E) and (F) reduce to f(n) = f(x) and f(n) = g(x), by

Thm*  a,z:, n:, s:({a...z}{1...n}Peg), n':.
Thm*  nn'
Thm*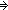  
Thm*  (h:({n+1...n'}Peg), i:{1...n'}.
Thm*  (n<i  (x:{a...z}. (s(?) {to n}  h {to n'})(x,i) = h(i)))

and follow from x = n and (A) above.

QED

About: IF YOU CAN SEE THIS go to /sfa/Nuprl/Shared/Xindentation_hack_doc.html