Selected Objects
| Introduction | Introductory Remarks |
| COM | hanoi_basic_problem
|
The Towers of Hanoi - formulating the problem
... |
| COM | hanoi_basic_solution
|
The Towers of Hanoi - the standard recursive solution
... |
| COM | hanoi_basic_solution_cont
|
Standard Solution made Explicit
... |
| COM | hanoi_oddrec_solution
|
A Non-standard Recursive Solution
... |
| COM | hanoi_std_optimal
|
Standard Solution is Optimal
... |
| COM | hanoi_std_simplerdata
|
Deriving Simpler Output Data
... |
| COM | hanoi_std_extraction
|
Automatic Extraction of a Solution
... |
| def | hanoi_PEG
|
(the three pegs used in The Towers of Hanoi Problem)
Peg == {1...3} |
| def | eq_hanoi_PEG
|
p=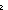 q == if p=q q == if p=q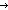 true true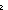 ; false ; false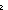 fi fi |
| THM | hanoi_pegseq_analemma
|
Given a sequence of pegs, perhaps with repititions, that starts with one and ends with another, there is a maximal prefix sequence every entry of which is the start peg, and there is a maximal suffix sequence every entry of which is the ending peg.
 p,q:Peg. p,q:Peg.
p  q q
 
( a: a: , z:{a...}, f:({a...z} , z:{a...}, f:({a...z}  Peg). Peg).
(f(a) = p & f(z) = q
( 
(( x:{a...z-1}, y:{x+1...z}. x:{a...z-1}, y:{x+1...z}.
((( u:{a...x}. f(u) = p) & f(x+1) u:{a...x}. f(u) = p) & f(x+1)  p & f(y-1) p & f(y-1)  q & ( q & ( u:{y...z}. f(u) = q))) u:{y...z}. f(u) = q))) |
| def | hanoi_otherpeg
|
(given distinct Pegs, the other (third) peg)
otherPeg(x; y) == 6-(x+y) |
| THM | hanoi_otherpeg_only
|
 x,y,z:Peg. x x,y,z:Peg. x  y y   x x  z z   y y  z z   x = otherPeg(y; z) x = otherPeg(y; z) |
| THM | hanoi_otherpeg_sym
|
 x,y:Peg. x x,y:Peg. x  y y   otherPeg(x; y) = otherPeg(y; x) otherPeg(x; y) = otherPeg(y; x) |
| THM | hanoi_otherpeg_diff1
|
 x,y:Peg. x x,y:Peg. x  y y   otherPeg(x; y) otherPeg(x; y)  x x |
| THM | hanoi_otherpeg_diff2
|
 x,y:Peg. x x,y:Peg. x  y y   otherPeg(x; y) otherPeg(x; y)  y y |
| THM | hanoi_otherpeg_diff3
|
 x,y:Peg. x x,y:Peg. x  y y   x x  otherPeg(x; y) otherPeg(x; y) |
| THM | hanoi_otherpeg_diff4
|
 x,y:Peg. x x,y:Peg. x  y y   y y  otherPeg(x; y) otherPeg(x; y) |
| def | hanoi_peg_perm
|
(permute the pegs, mapping p to r and q to s)
permute(p to r ; q to s)(u) == if u=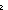 p p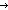 r ; u= r ; u=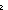 q q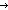 s else otherPeg(r; s) fi s else otherPeg(r; s) fi |
| THM | hanoi_peg_perm_is_inj
|
 p,r,q,s:Peg. p p,r,q,s:Peg. p  q q   r r  s s   Inj(Peg; Peg; permute(p to r ; q to s)) Inj(Peg; Peg; permute(p to r ; q to s)) |
| THM | hanoi_peg_perm_comp1
|
 p,r,q,s:Peg. p p,r,q,s:Peg. p  q q   r r  s s   permute(p to r ; q to s)(p) = r permute(p to r ; q to s)(p) = r |
| THM | hanoi_peg_perm_comp2
|
 p,r,q,s:Peg. p p,r,q,s:Peg. p  q q   r r  s s   permute(p to r ; q to s)(q) = s permute(p to r ; q to s)(q) = s |
| def | hanoi_extend
|
(extending a stacking situation to larger disks by explicit stipulation of location for each new disk)
(f {to n}  f' {to n'})(i) == if i f' {to n'})(i) == if i 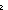 n n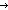 f(i) else f'(i) fi f(i) else f'(i) fi |
| THM | hanoi_extend_loweq
|
 n: n: , f:({1...n} , f:({1...n}  Peg), n': Peg), n': . .
n n' n'
 
( f':({n+1...n'} f':({n+1...n'}  Peg), i:{1...n'}. i Peg), i:{1...n'}. i n n   (f {to n} (f {to n}  f' {to n'})(i) = f(i)) f' {to n'})(i) = f(i)) |
| THM | hanoi_extend_higheq
|
 n: n: , f:({1...n} , f:({1...n}  Peg), n': Peg), n': . .
n n' n'
 
( f':({n+1...n'} f':({n+1...n'}  Peg), i:{1...n'}. n<i Peg), i:{1...n'}. n<i   (f {to n} (f {to n}  f' {to n'})(i) = f'(i)) f' {to n'})(i) = f'(i)) |
| def | hanoi_step_at
|
Characterization of legitimate moves in the Towers of Hanoi.
Stacking situations f and g differ just about where disk k is, and none of the disks smaller than k is in the way.
Moving disk k of n takes f to g
== ( i:{1...n}. f(i) = g(i) i:{1...n}. f(i) = g(i)  Peg Peg 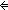  i i  k) k)
== & ( i:{1...k-1}. f(i) i:{1...k-1}. f(i)  f(k) f(k)  Peg & g(i) Peg & g(i)  g(k) g(k)  Peg) Peg) |
| THM | hanoi_step_at_same
|
Moving one disk leaves the others in place.
 n: n: , f,g:({1...n} , f,g:({1...n}  Peg), k,i:{1...n}. Peg), k,i:{1...n}.
Moving disk k of n takes f to g   i i  k k   f(i) = g(i) f(i) = g(i) |
| THM | hanoi_step_at_change2
|
Moving one disk changes its peg.
 n: n: , f,g:({1...n} , f,g:({1...n}  Peg), k:{1...n}. Peg), k:{1...n}.
Moving disk k of n takes f to g   f(k) f(k)  g(k) g(k) |
| THM | hanoi_step_at_otherpeg
|
Moving one disk leaves the smaller disks in place.
 n: n: , f,g:({1...n} , f,g:({1...n}  Peg), k:{1...n}. Peg), k:{1...n}.
Moving disk k of n takes f to g
 
f = ( i.otherPeg(f(k); g(k))) i.otherPeg(f(k); g(k)))  {1...k-1} {1...k-1}  Peg Peg |
| THM | hanoi_step_at_unique
|
Moving one disk moves only that disk.
 n: n: , f,g:({1...n} , f,g:({1...n}  Peg), i,k:{1...n}. Peg), i,k:{1...n}.
Moving disk k of n takes f to g   f(i) f(i)  g(i) g(i)   i = k i = k |
| THM | hanoi_step_at_change
|
If moving some disk converts f to g then the conversion if effected by moving whatever disk they disagree on.
 n: n: , f,g:({1...n} , f,g:({1...n}  Peg), j:{1...n}. Peg), j:{1...n}.
( k:{1...n}. Moving disk k of n takes f to g) k:{1...n}. Moving disk k of n takes f to g)
 
f(j)  g(j) g(j)   Moving disk j of n takes f to g Moving disk j of n takes f to g |
| THM | hanoi_step_at_sym
|
Disk moves can be reversed.
 n: n: , f,g:({1...n} , f,g:({1...n}  Peg), k:{1...n}. Peg), k:{1...n}.
Moving disk k of n takes f to g   Moving disk k of n takes g to f Moving disk k of n takes g to f |
| THM | hanoi_step_at_diff
|
Moving a disk changes its location.
 n: n: , f,g:({1...n} , f,g:({1...n}  Peg), k:{1...n}. Peg), k:{1...n}.
Moving disk k of n takes f to g   f(k) f(k)  g(k) g(k) |
| def | hanoi_seq
|
(the criterion for a sequence of stacking situations being a legitimate Hanoi Towers sequence)
s is a Hanoi(n disk) seq on a..z
==  x,x':{a...z}. x,x':{a...z}.
== x+1 = x'   ( ( k:{1...n}. Moving disk k of n takes s(x) to s(x')) k:{1...n}. Moving disk k of n takes s(x) to s(x')) |
| THM | hanoi_seq_core
(Proof Gloss) |
If you take an interior subsequence of a proper stacking sequence and remove the disks above a certain size, you'll be left with a proper stacking sequence.
 n': n': , n:{n'...}, a,z: , n:{n'...}, a,z: , s:({a...z} , s:({a...z}  {1...n} {1...n}  Peg). Peg).
s is a Hanoi(n disk) seq on a..z
 
( a',z':{a...z}. a',z':{a...z}.
(( x:{a'...z'}, i:{n'+1...n}. s(a',i) = s(x,i)) x:{a'...z'}, i:{n'+1...n}. s(a',i) = s(x,i))
( 
(s is a Hanoi(n' disk) seq on a'..z') |
| THM | hanoi_seq_permutepegs
(Proof Gloss) |
Permuting the pegs throughout a Hanoi sequence results in a Hanoi sequence.
 n: n: , a,z: , a,z: , s:({a...z} , s:({a...z}  {1...n} {1...n}  Peg). Peg).
s is a Hanoi(n disk) seq on a..z
 
( f:(Peg f:(Peg  Peg). Peg).
(Inj(Peg; Peg; f)   ( ( x,i. f(s(x,i))) is a Hanoi(n disk) seq on a..z) x,i. f(s(x,i))) is a Hanoi(n disk) seq on a..z) |
| def | hanoi_seq_deepen
|
(deepening a Hanoi sequence by adding larger disks to each of its individual stacking situations the same way)
(s(?) {to n}  h {to n'})(x) == s(x) {to n} h {to n'})(x) == s(x) {to n}  h {to n'} h {to n'} |
| THM | hanoi_seq_deepen_higheq
|
 a,z: a,z: , n: , n: , s:({a...z} , s:({a...z}  {1...n} {1...n}  Peg), n': Peg), n': . .
n n' n'
 
( h:({n+1...n'} h:({n+1...n'}  Peg), i:{1...n'}. Peg), i:{1...n'}.
(n<i   ( ( x:{a...z}. (s(?) {to n} x:{a...z}. (s(?) {to n}  h {to n'})(x,i) = h(i))) h {to n'})(x,i) = h(i))) |
| THM | hanoi_seq_deepen_loweq
|
 a,z: a,z: , n: , n: , s:({a...z} , s:({a...z}  {1...n} {1...n}  Peg), n': Peg), n': . .
n n' n'
 
( h:({n+1...n'} h:({n+1...n'}  Peg), i:{1...n'}. Peg), i:{1...n'}.
(i n n   ( ( x:{a...z}. (s(?) {to n} x:{a...z}. (s(?) {to n}  h {to n'})(x,i) = s(x,i))) h {to n'})(x,i) = s(x,i))) |
| THM | hanoi_seq_deepen_seq
(Proof Gloss) |
Deepening a Hanoi sequence results in a Hanoi sequence.
 a,z: a,z: , n: , n: , s:({a...z} , s:({a...z}  {1...n} {1...n}  Peg), n': Peg), n': . .
n n' n'
 
( h:({n+1...n'} h:({n+1...n'}  Peg). Peg).
(s is a Hanoi(n disk) seq on a..z
( 
((s(?) {to n}  h {to n'}) is a Hanoi(n' disk) seq on a..z) h {to n'}) is a Hanoi(n' disk) seq on a..z) |
| THM | hanoi_seq_shift
|
 n: n: , a,z,d: , a,z,d: , s:({a...z} , s:({a...z}  {1...n} {1...n}  Peg). Peg).
s is a Hanoi(n disk) seq on a..z
 
( x.s(x-d)) is a Hanoi(n disk) seq on a+d..z+d x.s(x-d)) is a Hanoi(n disk) seq on a+d..z+d |
| THM | hanoi_subseq
|
 n: n: , a,z: , a,z: , s:({a...z} , s:({a...z}  {1...n} {1...n}  Peg). Peg).
s is a Hanoi(n disk) seq on a..z
 
( a',z':{a...z}. s is a Hanoi(n disk) seq on a'..z') a',z':{a...z}. s is a Hanoi(n disk) seq on a'..z') |
| THM | hanoi_seq_shallower
|
 n': n': , n:{n'...}, a: , n:{n'...}, a: , z:{a...}, s:({a...z} , z:{a...}, s:({a...z}  {1...n} {1...n}  Peg). Peg).
s is a Hanoi(n disk) seq on a..z
 
( x:{a...z}, i:{n'+1...n}. s(a,i) = s(x,i)) x:{a...z}, i:{n'+1...n}. s(a,i) = s(x,i))   s is a Hanoi(n' disk) seq on a..z s is a Hanoi(n' disk) seq on a..z |
| def | hanoi_seq_join
|
(catenate sequence s1 ending at m with sequence s2 beginning with m+1)
(s1 @(m) s2)(x) == if x 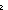 m m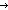 s1(x) else s2(x) fi s1(x) else s2(x) fi |
| THM | hanoi_seq_join_part1
|
 n: n: , m,a,z: , m,a,z: , s1:({a...m} , s1:({a...m}  {1...n} {1...n}  Peg), s2:({m+1...z} Peg), s2:({m+1...z}  {1...n} {1...n}  Peg), Peg),
 x:{a...m}. (s1 @(m) s2)(x) = s1(x) x:{a...m}. (s1 @(m) s2)(x) = s1(x) |
| THM | hanoi_seq_join_part2
|
 n: n: , m,a,z: , m,a,z: , s1:({a...m} , s1:({a...m}  {1...n} {1...n}  Peg), s2:({m+1...z} Peg), s2:({m+1...z}  {1...n} {1...n}  Peg), Peg),
 x:{m+1...z}. (s1 @(m) s2)(x) = s2(x) x:{m+1...z}. (s1 @(m) s2)(x) = s2(x) |
| THM | hanoi_seq_join_seq
(Proof Gloss) |
Joining two Hanoi sequences produces a Hanoi sequence if a single move takes the end of the first to the start of the second.
 n: n: , a,z: , a,z: , m:{a...z-1}, s1:({a...m} , m:{a...z-1}, s1:({a...m}  {1...n} {1...n}  Peg), Peg),
 s2:({m+1...z} s2:({m+1...z}  {1...n} {1...n}  Peg). Peg).
( k:{1...n}. Moving disk k of n takes s1(m) to s2(m+1)) k:{1...n}. Moving disk k of n takes s1(m) to s2(m+1))
 
s1 is a Hanoi(n disk) seq on a..m
 
s2 is a Hanoi(n disk) seq on m+1..z
 
(s1 @(m) s2) is a Hanoi(n disk) seq on a..z |
| THM | hanoi_general_exists_lemma1
(Proof Gloss) |
From a sequence of moves for one fewer disks we can derive one having the largest disk on the same peg at the beginning and the end.
 n: n: 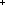 , f,g:({1...n} , f,g:({1...n}  Peg). Peg).
f(n) = g(n)
 
( a: a: , z:{a...}. , z:{a...}.
(( s:({a...z} s:({a...z}  {1...n-1} {1...n-1}  Peg). Peg).
((s is a Hanoi(n-1 disk) seq on a..z
((& s(a) = f  {1...n-1} {1...n-1}  Peg Peg
((& s(z) = g  {1...n-1} {1...n-1}  Peg) Peg)
( 
(( s:({a...z} s:({a...z}  {1...n} {1...n}  Peg). Peg).
((s is a Hanoi(n disk) seq on a..z & s(a) = f & s(z) = g)) |
| THM | hanoi_general_exists_lemma2
(Proof Gloss) |
A lemma about composing stacking situations into a Hanoi seqence, given one already has appropriate Hanoi sequences for one fewer disks.
 n: n: 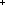 , a: , a: , z:{a...}, m:{a...z-1}, f,g:({1...n} , z:{a...}, m:{a...z-1}, f,g:({1...n}  Peg). Peg).
f(n)  g(n) g(n)
 
( s1:({a...m} s1:({a...m}  {1...n-1} {1...n-1}  Peg), s2:({m+1...z} Peg), s2:({m+1...z}  {1...n-1} {1...n-1}  Peg). Peg).
(s1 is a Hanoi(n-1 disk) seq on a..m
(& s1(a) = f  {1...n-1} {1...n-1}  Peg Peg
(& s2 is a Hanoi(n-1 disk) seq on m+1..z
(& s2(z) = g  {1...n-1} {1...n-1}  Peg Peg
(& s1(m) = s2(m+1)
(& ( i:{1...n-1}. s1(m,i) i:{1...n-1}. s1(m,i)  f(n) & s2(m+1,i) f(n) & s2(m+1,i)  g(n))) g(n)))
 
( r1:({a...m} r1:({a...m}  {1...n} {1...n}  Peg), r2:({m+1...z} Peg), r2:({m+1...z}  {1...n} {1...n}  Peg). Peg).
((r1 @(m) r2) is a Hanoi(n disk) seq on a..z & r1(a) = f & r2(z) = g) |
| def | hanoi_general_exists_lemma2PROG
|
HanoiHelper(n; s1; f; s2; g)
== <s1(?) {to n-1}  f {to n},s2(?) {to n-1} f {to n},s2(?) {to n-1}  g {to n}> g {to n}> |
| THM | hanoi_general_exists_lemma2PROGworks
|
 n: n: 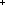 , a: , a: , z:{a...}, m:{a...z-1}, f,g:({1...n} , z:{a...}, m:{a...z-1}, f,g:({1...n}  Peg). Peg).
f(n)  g(n) g(n)
 
( s1:({a...m} s1:({a...m}  {1...n-1} {1...n-1}  Peg), s2:({m+1...z} Peg), s2:({m+1...z}  {1...n-1} {1...n-1}  Peg). Peg).
(s1 is a Hanoi(n-1 disk) seq on a..m
(& s1(a) = f  {1...n-1} {1...n-1}  Peg Peg
(& s2 is a Hanoi(n-1 disk) seq on m+1..z
(& s2(z) = g  {1...n-1} {1...n-1}  Peg Peg
(& s1(m) = s2(m+1)
(& ( i:{1...n-1}. s1(m,i) i:{1...n-1}. s1(m,i)  f(n) & s2(m+1,i) f(n) & s2(m+1,i)  g(n)) g(n))
( 
((HanoiHelper(n; s1; f; s2; g)/r1,r2.
(((r1 @(m) r2) is a Hanoi(n disk) seq on a..z & r1(a) = f & r2(z) = g)) |
| THM | hanoi_sol2_via_permshift
(Proof Gloss) |
There is a Hanoi sequence taking all the disks from any peg to any other.
 n: n: , p,q:Peg. , p,q:Peg.
p  q q
 
( z:{1...}, s:({1...z} z:{1...}, s:({1...z}  {1...n} {1...n}  Peg). Peg).
(s is a Hanoi(n disk) seq on 1..z & s(1) = ( i.p) & s(z) = ( i.p) & s(z) = ( i.q)) i.q)) |
| THM | hanoi_sol2_ala_general
(Proof Gloss) |
The Towers of Hanoi Problem is soluble.
 n: n: , p,q:Peg. , p,q:Peg.
p  q q
 
( a: a: . .
( z:{a...}, s:({a...z} z:{a...}, s:({a...z}  {1...n} {1...n}  Peg). Peg).
(s is a Hanoi(n disk) seq on a..z & s(a) = ( i.p) & s(z) = ( i.p) & s(z) = ( i.q)) i.q)) |
| def | hanoi_sol2_ala_generalPROG
|
HanoiSTD(n disks; from: p; to: q; indexing from: a)
== if n=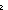 0 0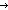 <a, <a, x,i. whatever> x,i. whatever>
== else HanoiSTD(n-1 disks; from: p; to: otherPeg(p; q); indexing from: a)/m,s1.
== else HanoiSTD(n-1 disks; from: otherPeg(p; q); to: q; indexing from: m+1)
== else /z,s2. <z,HanoiHelper(n; s1;  i.p; s2; i.p; s2;  i.q)/r1,r2. r1 @(m) r2> fi i.q)/r1,r2. r1 @(m) r2> fi
(recursive) |
| THM | hanoi_sol2_ala_generalPROGcomp
|
 n: n: 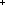 , p,q:Peg. , p,q:Peg.
p  q q
 
( a: a: . .
(HanoiSTD(n disks; from: p; to: q; indexing from: a)
(=
((HanoiSTD(n-1 disks; from: p; to: otherPeg(p; q); indexing from: a)/m,s1.
((HanoiSTD(n-1 disks; from: otherPeg(p; q); to: q; indexing from: m+1)/z,s2.
((<z,HanoiHelper(n; s1;  i.p; s2; i.p; s2;  i.q)/r1,r2. r1 @(m) r2>)) i.q)/r1,r2. r1 @(m) r2>)) |
| THM | hanoi_sol2_ala_generalPROGworks
|
 n: n: , p,q:Peg. , p,q:Peg.
p  q q
 
( a: a: . .
(HanoiSTD(n disks; from: p; to: q; indexing from: a)/z,s.
(s is a Hanoi(n disk) seq on a..z
(& s(a) = ( i.p) i.p)  {1...n} {1...n}  Peg Peg
(& s(z) = ( i.q) i.q)  {1...n} {1...n}  Peg) Peg) |
| THM | hanoi_general_exists
(Proof Gloss) |
This generalizes of The Towers of Hanoi Problem by not constraining the start and end positions of the disks.
There is a Hanoi sequence of moves for any possible starting and ending situations.
 n: n: , f,g:({1...n} , f,g:({1...n}  Peg), a: Peg), a: . .
 z:{a...}, s:({a...z} z:{a...}, s:({a...z}  {1...n} {1...n}  Peg). Peg).
s is a Hanoi(n disk) seq on a..z & s(a) = f & s(z) = g |
| THM | hanoi_sol2_via_general
|
Corollary of hanoi general exists.
The Towers of Hanoi Problem is soluble.
 n: n: , p,q:Peg. , p,q:Peg.
p  q q
 
( a: a: . .
( z:{a...}, s:({a...z} z:{a...}, s:({a...z}  {1...n} {1...n}  Peg). Peg).
(s is a Hanoi(n disk) seq on a..z & s(a) = ( i.p) & s(z) = ( i.p) & s(z) = ( i.q)) i.q)) |
| THM | hanoi_general_exists_lemma2PROG_endpoint
(Proof Gloss) |
The standard Hanoi Towers solution is a sequence whose length is 2 raised to the number of disks.
 n: n: , p,q:Peg. , p,q:Peg.
p  q q
 
( a: a: . 1of(HanoiSTD(n disks; from: p; to: q; indexing from: a)) = a+(2^n)-1) . 1of(HanoiSTD(n disks; from: p; to: q; indexing from: a)) = a+(2^n)-1) |
| THM | hanoi_sol2_analemma
(Proof Gloss) |
A nontrivial Hanoi sequence solving The Towers of Hanoi Problem can be broken into two parts, the first of which keeps the largest disk on the starting peg and the second of which keeps it on the ending peg.
 n: n: 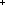 , p,q:Peg. , p,q:Peg.
p  q q
 
( a: a: , z:{a...}, s:({a...z} , z:{a...}, s:({a...z}  {1...n} {1...n}  Peg). Peg).
(s is a Hanoi(n disk) seq on a..z & s(a) = ( i.p) & s(z) = ( i.p) & s(z) = ( i.q) i.q)
( 
(( x:{a...z-1}, y:{x+1...z}, p',q':Peg. x:{a...z-1}, y:{x+1...z}, p',q':Peg.
((( u:{a...x}. s(u,n) = p) & ( u:{a...x}. s(u,n) = p) & ( u:{y...z}. s(u,n) = q) u:{y...z}. s(u,n) = q)
((& s(x) = ( i.p') i.p')  {1...n-1} {1...n-1}  Peg & s(y) = ( Peg & s(y) = ( i.q') i.q')  {1...n-1} {1...n-1}  Peg Peg
((& p  p' p'
((& q  q')) q')) |
| THM | hanoi_sol2_lb
(Proof Gloss) |
The length of any Hanoi sequence solving The Towers of Hanoi Problem is at least 2 raised to the number of disks.
 n: n: , p,q:Peg. , p,q:Peg.
p  q q
 
( a: a: , z:{a...}, s:({a...z} , z:{a...}, s:({a...z}  {1...n} {1...n}  Peg). Peg).
(s is a Hanoi(n disk) seq on a..z & s(a) = ( i.p) & s(z) = ( i.p) & s(z) = ( i.q) i.q)
( 
((2^n) z-a+1) z-a+1) |