The Towers of Hanoi - the standard recursive solution

We shall treat the basic problem very precisely and in various ways. Our starting point will be a proof that a solution is possible:

Thm*  n:, p,q:Peg.
Thm*  p  q
Thm*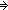  
Thm*  (a:. 
Thm*  (z:{a...}, s:({a...z}{1...n}Peg).
Thm*  (s is a Hanoi(n disk) seq on a..z & s(a) = (i.p) & s(z) = (i.q))

This theorem is stated entirely in terms of the formalizations introduced for the Towers of Hanoi Problem, and is carried out based purely on that formulation. This particular proof, however, digressing briefly from the standard solution, was derived from a generalization of the basic problem

Thm*  n:, f,g:({1...n}Peg), a:.
Thm*  z:{a...}, s:({a...z}{1...n}Peg).
Thm*  s is a Hanoi(n disk) seq on a..z & s(a) = f & s(z) = g

Gloss

to the effect that one can build a legitimate sequence of stacking situations leading from any stacking situation to any stacking situation. Implicit in this proof of the more general problem is a recursive procedure: If there are no disks then we're done, else see if the largest disk needs to me moved; if not, then just move the smaller disks according to this procedure. Otherwise, considering which peg the largest disk is on and which peg it should end up on, move all the smaller disks to the peg other than these two pegs, then move the largest disk, then move all the smaller disks according to this procedure.

The possibility of solving the standard problem follows from the more general solution, as realized by the first proof referenced above, but let us focus more narrowly on the standard solution. Here is a proof for the standard problem which directly imitates, but simplifies, the general solution rather than simply citing it as a lemma. We will more easily see the more specialized algorithm by examining this proof:

Thm*  n:, p,q:Peg.
Thm*  p  q
Thm*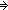  
Thm*  (a:. 
Thm*  (z:{a...}, s:({a...z}{1...n}Peg).
Thm*  (s is a Hanoi(n disk) seq on a..z & s(a) = (i.p) & s(z) = (i.q))

Gloss

See Standard Solution Explicitly for procedures that make these implicit procedures explicit.

About: IF YOU CAN SEE THIS go to /sfa/Nuprl/Shared/Xindentation_hack_doc.html