Thm*  n:, f,g:({1...n}Peg), a:.
Thm*  z:{a...}, s:({a...z}{1...n}Peg).
Thm*  s is a Hanoi(n disk) seq on a..z & s(a) = f & s(z) = g

The proof is by induction on n  . For the base case of 0 disks, no moves are needed and the starting situation is the ending situation and is the only situation possible, namely, no disks on any Peg. Given f, g  {1...0}Peg, a  , as hypothesized, choose a itself for z and (x.f) for s. Then (x.f) is a Hanoi(0 disk) seq on a..a, trivially since there are not two successive positions in {a...a}. And the rest of the base case (s(a) = f & s(z) = g) follows since there is only one zero-disk situation, i.e. only one function in {1...0}Peg -- see Void.

Now taking as our inductive hypothesis

f,g:({1...n-1}Peg), a:.
z:{a...}, s:({a...z}{1...n-1}Peg).
s is a Hanoi(n-1 disk) seq on a..z & s(a) = f & s(z) = g

and assuming f, g  {1...n}Peg, a  , we need to show

(*) z:{a...}, s:({a...z}{1...n}Peg).
(*) s is a Hanoi(n disk) seq on a..z & s(a) = f & s(z) = g

Is the largest disk already in place? That is, is f(n) = g(n)? If so, then instantiating the inductive hypothesis on f, g, and a gives a z such that

s:({a...z}{1...n-1}Peg). 
s is a Hanoi(n-1 disk) seq on a..z
& s(a) = f  {1...n-1}Peg
& s(z) = g  {1...n-1}Peg

which will suffice to show our goal by the following lemma

Thm*  n:, f,g:({1...n}Peg).
Thm*  f(n) = g(n)
Thm*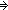  
Thm*  (a:, z:{a...}.
Thm*  ((s:({a...z}{1...n-1}Peg). 
Thm*  ((s is a Hanoi(n-1 disk) seq on a..z
Thm*  ((& s(a) = f  {1...n-1}Peg
Thm*  ((& s(z) = g  {1...n-1}Peg)
Thm*  (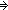
Thm*  ((s:({a...z}{1...n}Peg). 
Thm*  ((s is a Hanoi(n disk) seq on a..z & s(a) = f & s(z) = g))

Gloss

If, on the other hand, f(n)  g(n), then we can (and shortly we will) show that

(A) z:{a...}, m:{a...z-1}, s1:({a...m}{1...n}Peg),
(A) s2:({m+1...z}{1...n}Peg).
(A) (s1 @(m) s2) is a Hanoi(n disk) seq on a..z & s1(a) = f & s2(z) = g

where s1 @(m) s2 is simply a joining together of Hanoi sequences s1 and s2. And from (A) our conclusion (*) follows, by using s1 @(m) s2 for s, since (s1 @(m) s2)(a) and (s1 @(m) s2)(z) reduce to s1(a) and s2(z). See Joining.

Continued at hanoi general exists gloss cont

About: IF YOU CAN SEE THIS go to /sfa/Nuprl/Shared/Xindentation_hack_doc.html