The operation s1 @(m) s2 stands for chaining together a sequence ending at position m together with another one beginning at position m+1.

Def  (s1 @(m) s2)(x) == if xm s1(x) else s2(x) fi

Thm*  n:, m,a,z:, s1:({a...m}{1...n}Peg), s2:({m+1...z}{1...n}Peg).
Thm*  (s1 @(m) s2)  {a...z}{1...n}Peg

The rewrite lemmas for simplifying such a composite sequence at each position are

Thm*  n:, m,a,z:, s1:({a...m}{1...n}Peg), s2:({m+1...z}{1...n}Peg),
Thm*  x:{a...m}. (s1 @(m) s2)(x) = s1(x)

Thm*  n:, m,a,z:, s1:({a...m}{1...n}Peg), s2:({m+1...z}{1...n}Peg),
Thm*  x:{m+1...z}. (s1 @(m) s2)(x) = s2(x)

The point of joining sequences is to get a proper Hanoi sequence from two Hanoi subsequences:

Thm*  n:, a,z:, m:{a...z-1}, s1:({a...m}{1...n}Peg),
Thm*  s2:({m+1...z}{1...n}Peg).
Thm*  (k:{1...n}. Moving disk k of n takes s1(m) to s2(m+1))
Thm*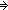  
Thm*  s1 is a Hanoi(n disk) seq on a..m
Thm*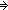  
Thm*  s2 is a Hanoi(n disk) seq on m+1..z
Thm*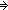  
Thm*  (s1 @(m) s2) is a Hanoi(n disk) seq on a..z

Gloss

which works because the moves in the two subsequences are independent, and a single move takes the end of the first to the start of the second.

About: IF YOU CAN SEE THIS go to /sfa/Nuprl/Shared/Xindentation_hack_doc.html