| | Some definitions of interest. |
|
| hanoi_seq | Def s is a Hanoi(n disk) seq on a..z
Def ==  x,x':{a...z}. x,x':{a...z}.
Def == x+1 = x' 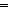 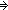 ( (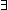 k:{1...n}. Moving disk k of n takes s(x) to s(x')) k:{1...n}. Moving disk k of n takes s(x) to s(x')) |
| | | Thm*  n: n: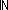 , a,z: , a,z: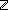 , s:({a...z} , s:({a...z} 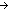 {1...n} {1...n} 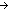 Peg). Peg).
Thm* s is a Hanoi(n disk) seq on a..z 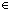 Prop Prop |
|
| hanoi_step_at | Def Moving disk k of n takes f to g
Def == ( i:{1...n}. f(i) = g(i) i:{1...n}. f(i) = g(i) 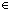 Peg Peg 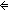 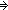 i i 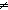 k) k)
Def == & ( i:{1...k-1}. f(i) i:{1...k-1}. f(i) 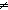 f(k) f(k) 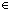 Peg & g(i) Peg & g(i) 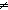 g(k) g(k) 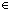 Peg) Peg) |
| | | Thm*  n: n: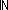 , f,g:({1...n} , f,g:({1...n} 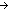 Peg), k:{1...n}. Peg), k:{1...n}.
Thm* Moving disk k of n takes f to g 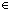 Prop Prop |
|
| hanoi_PEG | Def Peg == {1...3} |
| | | Thm* Peg 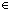 Type Type |
|
| hanoi_seq_join | Def (s1 @(m) s2)(x) == if x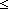 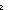 m m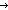 s1(x) else s2(x) fi s1(x) else s2(x) fi |
| | | Thm*  n: n: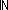 , m,a,z: , m,a,z: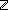 , s1:({a...m} , s1:({a...m} 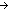 {1...n} {1...n} 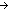 Peg), s2:({m+1...z} Peg), s2:({m+1...z} 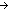 {1...n} {1...n} 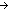 Peg). Peg).
Thm* (s1 @(m) s2) 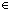 {a...z} {a...z} 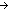 {1...n} {1...n} 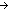 Peg Peg |
|
| int_iseg | Def {i...j} == {k: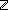 | i | i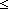 k & k k & k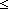 j } j } |
| | | Thm*  i,j: i,j: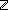 . {i...j} . {i...j} 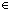 Type Type |
|
| le_int | Def i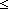 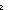 j == j ==  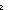 j< j<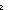 i i |
| | | Thm*  i,j: i,j: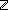 . (i . (i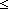 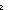 j) j) 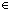 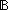 |
|
| nat | Def 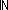 == {i: == {i: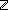 | 0 | 0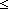 i } i } |
| | | Thm* 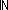 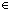 Type Type |