Thm*  a,z:, n:, s:({a...z}{1...n}Peg), n':.
Thm*  nn'
Thm*  
Thm*  (h:({n+1...n'}Peg). 
Thm*  (s is a Hanoi(n disk) seq on a..z
Thm*  (
Thm*  ((s(?) {to n}  h {to n'}) is a Hanoi(n' disk) seq on a..z)

In light of

Def  s is a Hanoi(n disk) seq on a..z
Def  == x,x':{a...z}.
Def  == x+1 = x'  (k:{1...n}. Moving disk k of n takes s(x) to s(x'))

we need to show that for k  {1...n}, supposing Moving disk k of n takes s(x) to s(x'),

Moving disk k of n'
takes (s(?) {to n}  h {to n'})(x) to (s(?) {to n}  h {to n'})(x'),

that is each move in the original sequence corresponds to moving the same disk in the deepened sequence.
By expanding the definition

Def  Moving disk k of n takes f to g
Def  == (i:{1...n}. f(i) = g(i)  Peg  i  k)
Def  == & (i:{1...k-1}. f(i)  f(k)  Peg & g(i)  g(k)  Peg)

our problem reduces to showing implications between the corresponding conjuncts, namely, that

(A) (i:{1...n}. s(x,i) = s(x',i)  i  k)
(A) 
(A) (i:{1...n'}. 
(A) ((s(?) {to n}  h {to n'})(x,i) = (s(?) {to n}  h {to n'})(x',i)  i  k)

and

(B) (i:{1...k-1}. s(x,i)  s(x,k) & s(x',i)  s(x',k))
(B) 
(B) (i:{1...k-1}. 
(B) ((s(?) {to n}  h {to n'})(x,i)  (s(?) {to n}  h {to n'})(x,k)
(B) (& (s(?) {to n}  h {to n'})(x',i)  (s(?) {to n}  h {to n'})(x',k))

The second of these two entailments (B) follows by (rewriting the conclusion with)

Thm*  a,z:, n:, s:({a...z}{1...n}Peg), n':.
Thm*  nn'
Thm*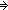  
Thm*  (h:({n+1...n'}Peg), i:{1...n'}.
Thm*  (in  (x:{a...z}. (s(?) {to n}  h {to n'})(x,i) = s(x,i)))

which simply says deepening leaves the the smaller disks in place. Entailment (A) will require a case split on the size of the disk: assume that i:{1...n}. s(x,i) = s(x',i)  i  k and that i  {1...n'}. Then we need to show that

(s(?) {to n}  h {to n'})(x,i) = (s(?) {to n}  h {to n'})(x',i)  i  k

If in then we can rewrite the goal, by the same fact used to rewrite (B) above, to

s(x,i) = s(x',i)  i  k

which follows from the antecedent of (A). Otherwise, with n<i, can rewrite the our goal by

Thm*  a,z:, n:, s:({a...z}{1...n}Peg), n':.
Thm*  nn'
Thm*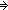  
Thm*  (h:({n+1...n'}Peg), i:{1...n'}.
Thm*  (n<i  (x:{a...z}. (s(?) {to n}  h {to n'})(x,i) = h(i)))

down to h(i) = h(i)  i  k which follows trivally from k  {1...n}.

QED

About: IF YOU CAN SEE THIS go to /sfa/Nuprl/Shared/Xindentation_hack_doc.html