More specifically, the whole sequence s of states indexed by {a...z} can be broken into parts indexed by {a...x} and {y...z}, the first of which keeps the largest disk (n) on the starting peg (p), removing smaller disks ({1...n-1}) to another peg (p'), and the second of which keeps it on the ending peg (q), removing all smaller disks from another peg (q').

Thm*  n:, p,q:Peg.
Thm*  p  q
Thm*  
Thm*  (a:, z:{a...}, s:({a...z}{1...n}Peg).
Thm*  (s is a Hanoi(n disk) seq on a..z & s(a) = (i.p) & s(z) = (i.q)
Thm*  (
Thm*  ((x:{a...z-1}, y:{x+1...z}, p',q':Peg.
Thm*  (((u:{a...x}. s(u,n) = p) & (u:{y...z}. s(u,n) = q)
Thm*  ((& s(x) = (i.p')  {1...n-1}Peg & s(y) = (i.q')  {1...n-1}Peg
Thm*  ((& p  p'
Thm*  ((& q  q'))

Given n  , z  {a...}, and assuming p  q, then by applying an analysis lemma for mere peg sequences

Thm*  p,q:Peg.
Thm*  p  q
Thm*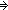  
Thm*  (a:, z:{a...}, f:({a...z}Peg).
Thm*  (f(a) = p & f(z) = q
Thm*  (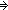
Thm*  ((x:{a...z-1}, y:{x+1...z}.
Thm*  (((u:{a...x}. f(u) = p)
Thm*  ((& f(x+1)  p
Thm*  ((& f(y-1)  q
Thm*  ((& (u:{y...z}. f(u) = q)))

That is: Given a sequence of pegs, perhaps with repititions, that starts with one and ends with another, there is a maximal prefix sequence every entry of which is the start peg, and there is a maximal suffix sequence every entry of which is the ending peg.

we infer that

(A) f:({a...z}Peg). 
(A) f(a) = p & f(z) = q
(A) 
(A) (x:{a...z-1}, y:{x+1...z}.
(A) ((u:{a...x}. f(u) = p) & f(x+1)  p & f(y-1)  q & (u:{y...z}. f(u) = q))

and further assuming that

(B) s is a Hanoi(n disk) seq on a..z

(C) s(a) = (i.p)

(D) s(z) = (i.q)

we must show that

(*) x:{a...z-1}, y:{x+1...z}, p',q':Peg.
(*) (u:{a...x}. s(u,n) = p) & (u:{y...z}. s(u,n) = q)
(*) & s(x) = (i.p')  {1...n-1}Peg & s(y) = (i.q')  {1...n-1}Peg
(*) & p  p'
(*) & q  q'

Continued at hanoi sol2 analemma gloss cont

About: IF YOU CAN SEE THIS go to /sfa/Nuprl/Shared/Xindentation_hack_doc.html