Thm*  n:, a,z:, s:({a...z}{1...n}Peg).
Thm*  s is a Hanoi(n disk) seq on a..z
Thm*  
Thm*  (f:(PegPeg). 
Thm*  (Inj(Peg; Peg; f)  (x,i. f(s(x,i))) is a Hanoi(n disk) seq on a..z)

We need to show that

s is a Hanoi(n disk) seq on a..z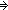

(x,i. f(s(x,i))) is a Hanoi(n disk) seq on a..z

which reduces by definition to showing that for x+1 = x'

Moving disk k of n takes s(x) to s(x')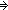

Moving disk k of n takes i.f(s(x,i)) to i.f(s(x',i))

Again by definition this reduces to showing four things:

i:{1...n}. s(x,i) = s(x',i)  f(s(x,i)) = f(s(x',i)),

which is trivial (equal arguments, equal results);

i:{1...n}. f(s(x,i)) = f(s(x',i))  s(x,i) = s(x',i),
i:{1...k-1}. f(s(x,i)) = f(s(x,k))  s(x,i) = s(x,k), and
i:{1...k-1}. f(s(x',i)) = f(s(x',k))  s(x',i) = s(x',k),

which all follow from Inj(Peg; Peg; f).

QED

About: IF YOU CAN SEE THIS go to /sfa/Nuprl/Shared/Xindentation_hack_doc.html