This is equivalent to the last index being the first index plus (2^n1)-1.

Thm*  n:, p,q:Peg.
Thm*  p  q
Thm*  
Thm*  (a:. 
Thm*  (1of(HanoiSTD(n disks; from: p; to: q; indexing from: a)) = a+(2^n)-1)

The proof is by less-than induction over . Under inductive hypothesis

n1:. 
n1<n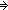

(p,q:Peg.
(p  q
(
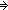
((a:. 1of(HanoiSTD(n1 disks; from: p; to: q; indexing from: a)) = a+(2^n1)-1))

and assuming p  q we need to show

1of(HanoiSTD(n disks; from: p; to: q; indexing from: a)) = a+(2^n)-1

Keeping in mind that (x,i. whatever) =   Top, if n = 0 then this goal reduces to a = a+1-1, and if n  0 then our goal reduces to

1of(HanoiSTD(n-1 disks; from: p; to: otherPeg(p; q); indexing from: a)/m,s1.
HanoiSTD(n-1 disks; from: otherPeg(p; q); to: q; indexing from: m+1)/z,s2.
<z,HanoiHelper(n; s1; i.p; s2; i.q)/r1,r2. r1 @(m) r2>)
=
a+2(2^(n-1))-1

By applying the inductive hypothesis we get

(A) 1of(HanoiSTD(n-1 disks; from: p; to: otherPeg(p; q); indexing from: a))
(A) =
(A) a+(2^(n-1))-1

then letting <m,s1> = HanoiSTD(n-1 disks; from: p; to: otherPeg(p; q); indexing from: a) we get

(B) m = 1of(HanoiSTD(n-1 disks; from: p; to: otherPeg(p; q); indexing from: a))

and our goal simplifies to

1of(HanoiSTD(n-1 disks; from: otherPeg(p; q); to: q; indexing from: m+1)/z,s2.
<z,HanoiHelper(n; s1; i.p; s2; i.q)/r1,r2. r1 @(m) r2>)
=
a+2(2^(n-1))-1

And applying the inductive hypothesis again we get

(C) 1of(HanoiSTD(n-1 disks; from: otherPeg(p; q); to: q; indexing from: m+1))
(C) =
(C) m+1+(2^(n-1))-1

Then letting <z,s2> = HanoiSTD(n-1 disks; from: otherPeg(p; q); to: q; indexing from: m+1) we get

(D) z
(D) =
(D) 1of(HanoiSTD(n-1 disks; from: otherPeg(p; q); to: q; indexing from: m+1))

and our goal simplifies further to

z = a+2(2^(n-1))-1

which follows by arithmetic from (D), (C), (B), and (A).

QED

About: IF YOU CAN SEE THIS go to /sfa/Nuprl/Shared/Xindentation_hack_doc.html